GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG
A. TÓM TẮT KIẾN THỨC CƠ BẢN
I – GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG ![]()
1. Định nghĩa
Trên đường tròn lượng giác cho cung ![]() có sđ
có sđ ![]() (còn viết ..)
(còn viết ..)
![]() Tung độ
Tung độ ![]()
![]()
![]() của điểm
của điểm ![]() gọi là sin của
gọi là sin của ![]() và kí hiệu là
và kí hiệu là ![]()
![]()
![]() Hoành độ
Hoành độ ![]() của điểm
của điểm ![]() gọi là côsin của
gọi là côsin của ![]() và kí hiệu là
và kí hiệu là ![]()
![]()
![]() Nếu
Nếu ![]() tỉ số
tỉ số  gọi là tang của
gọi là tang của ![]() và kí hiệu là
và kí hiệu là ![]() (người ta còn dùng kí hiệu
(người ta còn dùng kí hiệu ![]() )
)

![]() Nếu
Nếu ![]() tỉ số
tỉ số 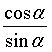 gọi là côtang của
gọi là côtang của ![]() và kí hiệu là
và kí hiệu là ![]() (người ta còn dùng kí hiệu
(người ta còn dùng kí hiệu ![]() ):
): 
Các giá trị ![]() được gọi là các giá trị lượng giác của cung
được gọi là các giá trị lượng giác của cung ![]()
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
2. Hệ quả
1) ![]() và
và ![]() xác định với mọi
xác định với mọi ![]() Hơn nữa, ta có
Hơn nữa, ta có

2) Vì ![]()
![]() nên ta có
nên ta có

3) Với mọi ![]() mà
mà ![]() đều tồn tại
đều tồn tại ![]() và
và ![]() sao cho
sao cho ![]() và
và ![]()
4) ![]() xác định với mọi
xác định với mọi 
5) ![]() xác định với mọi
xác định với mọi ![]()
6) Dấu của các giá trị lượng giác của góc ![]() phụ thuộc vào vị trí điểm cuối của cung
phụ thuộc vào vị trí điểm cuối của cung ![]() trên đường tròn lượng giác.
trên đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
| Góc phần tư
Giá trị lượng giác |
I | II | III | IV |
Mẹo ghi nhớ: “Nhất cả, nhị sin, tam tan, tứ cos”
3. Giá trị lượng giác của các cung đặc biệt
| Góc |
0 | |||||||||
| 00 | 300 | 450 | 600 | 900 | 1200 | 1350 | 1800 | 2700 | 3600 | |
| 0 | 1 | 0 | –1 | 0 | ||||||
| 1 | 0 | .. |  |
–1 | 0 | 1 | ||||
| 0 | 1 | –1 | 0 | 0 | ||||||
| 1 | 0 |  |
–1 | 0 |

II – Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG
1. Ý nghĩa hình học của ![]()
Từ ![]() vẽ tiếp tuyến
vẽ tiếp tuyến ![]() với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại
với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại ![]() .
.
Gọi ![]() là giao điểm của
là giao điểm của ![]() với trục
với trục ![]()
![]() được biểu diễn bởi độ dài đại số của vectơ
được biểu diễn bởi độ dài đại số của vectơ ![]() trên trục
trên trục ![]() Viết:
Viết: ![]()
Trục ![]() được gọi là trục tang.
được gọi là trục tang.
2. Ý nghĩa hình học của ![]()
Từ ![]() vẽ tiếp tuyến
vẽ tiếp tuyến ![]() với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại
với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại ![]() .
.
Gọi ![]() là giao điểm của
là giao điểm của ![]() với trục
với trục ![]()
![]() được biểu diển bởi độ dài đại số của vectơ
được biểu diển bởi độ dài đại số của vectơ ![]() trên trục
trên trục ![]() . Viết:
. Viết: ![]()
Trục ![]() được gọi là trục côtang.
được gọi là trục côtang.
Nhận xét: 
III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC
1. Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
![]()
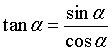 ,
, 
 ,
, ![]()
![]()




![]()
2. Giá trị lượng giác của các cung có liên quan đặc biệt
| Góc đối nhau ( |
Góc bù nhau( |
Góc phụ nhau( ) ) |
 |
||
 |
||
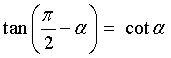 |
||
 |
| Góc hơn kém |
Góc hơn kém  ) ) |
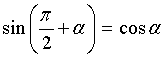 |
|
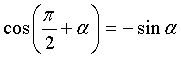 |
|
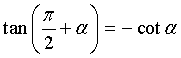 |
|
 |
Chú ý: Để nhớ nhanh các công thức trên ta nhớ câu: ” cos – đối, sin – bù, phụ – chéo, hơn kém ![]() tang côtang, hơn kém
tang côtang, hơn kém ![]() chéo sin”. Với nguyên tắc nhắc đến giá trị nào thì nó bằng còn không nhắc thì đối.
chéo sin”. Với nguyên tắc nhắc đến giá trị nào thì nó bằng còn không nhắc thì đối.
B. CÁC DẠNG TOÁN:
DẠNG 1: XÁC ĐỊNH DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC
I. PHƯƠNG PHÁP: Dấu của các giá trị lượng giác của góc ![]() phụ thuộc vào vị trí điểm cuối (điểm ngọn) của cung
phụ thuộc vào vị trí điểm cuối (điểm ngọn) của cung ![]() trên đường tròn lượng giác. Vì thế cần xác định vị trí điểm M trên đường tròn lượng giác rồi sử dụng bảng xét dấu các giá trị lượng giác.
trên đường tròn lượng giác. Vì thế cần xác định vị trí điểm M trên đường tròn lượng giác rồi sử dụng bảng xét dấu các giá trị lượng giác.
Bảng xác định dấu của các giá trị lượng giác
| Vị trí điểm M thuộc
góc phần tư Giá trị lượng giác |
I | II | III | IV |
II. VÍ DỤ MINH HỌA:
Cho  . Xác định dấu của các biểu thức sau:
. Xác định dấu của các biểu thức sau:
a)  b)
b) 
![]()
c)  d)
d) 
Lời giải
a) Ta có 
![]()

![]()

b) Ta có 
![]()

![]()

c) Ta có 
![]()

![]()

Và 
![]()
![]()
Vậy  .
.
d) Ta có 
![]()


![]()
 suy ra
suy ra ![]() .
.
Vậy 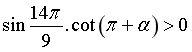 .
.