PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Ví dụ 1: Xác định vị trí tương đối của ![]() đường thẳng sau đây:
đường thẳng sau đây:
![]() :
: ![]() và
và ![]() :
: ![]() .
.
A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt nhau.
Hướng dẫn giải
Chọn A.
Cách 1: Giải hệ phương trình thấy vô nghiệm nên hai đường thẳng song song
Cách 2: Đường thẳng ![]() có vtpt
có vtpt ![]() và
và ![]() có vtpt
có vtpt ![]() .
.
Hai đường thẳng ![]() ,
, ![]() có
có ![]() và
và ![]() nên hai đường thẳng này song song
nên hai đường thẳng này song song
Ví dụ 2: Đường thẳng ![]() cắt đường thẳng nào sau đây?
cắt đường thẳng nào sau đây?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Hướng dẫn giải
Chọn A.
![]() và
và ![]() có
có 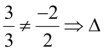 cắt
cắt ![]()
Ví dụ 3: Hai đường thẳng ![]() cắt nhau tại điểm có toạ độ:
cắt nhau tại điểm có toạ độ:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() .
.
Hướng dẫn giải
Chọn A.
Giải hệ phương trình 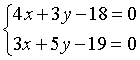 ta được
ta được 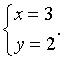
Ví dụ 4: Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Hướng dẫn giải
Chọn D.
![]() và đường thẳng
và đường thẳng ![]() không song song vì
không song song vì  .
.
Ví dụ 5: Hai đường thẳng ![]() song song khi và chỉ khi:
song song khi và chỉ khi:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Hướng dẫn giải
Chọn C.
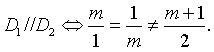
Khi ![]() ta có:
ta có: 
Khi ![]() ta có:
ta có: 
Ví dụ 6: Cho 3 đường thẳng ![]() Để ba đường thẳng này đồng qui thì giá trị thích hợp của
Để ba đường thẳng này đồng qui thì giá trị thích hợp của ![]() là:
là:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Hướng dẫn giải:
Chọn B.
Giao điểm của ![]() và
và ![]() là nghiệm của hệ
là nghiệm của hệ 
Vậy ![]() cắt
cắt ![]() tại
tại ![]()
Để 3 đường thẳng ![]() đồng quy thì
đồng quy thì ![]() phải đi qua điểm
phải đi qua điểm ![]()
![]() thỏa phương trình
thỏa phương trình ![]()
![]()
Ví dụ 7: Cho ![]() điểm
điểm ![]() . Tìm tọa độ giao điểm của
. Tìm tọa độ giao điểm của ![]() đường thẳng
đường thẳng ![]() và
và ![]()
A. ![]() . B.
. B. 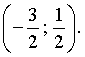
C. ![]() . D. Không có giao điểm.
. D. Không có giao điểm.
Hướng dẫn giải
Chọn D.
![]() có vectơ chỉ phương là
có vectơ chỉ phương là ![]() và
và ![]() có vectơ chỉ phương là
có vectơ chỉ phương là ![]() .
.
Ta có: ![]() và
và ![]() cùng phương nên
cùng phương nên ![]() và
và ![]() không có giao điểm.
không có giao điểm.
Ví dụ 8: Xác định vị trí tương đối của 2 đường thẳng: ![]()
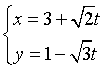 và
và ![]()
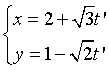
A. Song song nhau. B. Cắt nhau nhưng không vuông góc.
C. Vuông góc nhau. D. Trùng nhau.
Hướng dẫn giải
Chọn B.
Ta có: ![]() ,
, ![]() không cùng phương và
không cùng phương và ![]() nên
nên ![]() Cắt nhau nhưng không vuông góc
Cắt nhau nhưng không vuông góc