BÀI TOÁN VẬN DỤNG CAO CHUYÊN ĐỀ HÀM SỐ MŨ, LÔGARIT
Ở chương này những bài toán vận dụng cao sẽ rơi vào các dạng bài Lãi suất, dạng bài tính số chữ số của một số …
CHỦ ĐỀ 1.
TÍNH SỐ CHỮ SỐ CỦA MỘT SỐ TỰ NHIÊN
Sau đây chúng ta cùng nghiên cứu một ứng dụng của Logarit tron việc tính số các chữ số của một số tự nhiên.
Đầu tiên xin nhắc lại khái niệm thế nào là phần nguyên của một số.
1. Phần nguyên của một số:
Xét số thức A, số nguyên lớn nhất mà không vượt quá A người ta gọi là phần nguyên của A và kí hiệu là [A].
Như vậy dễ thấy 
.
2. Công thức tính số các chữ số của một số tự nhiên:
Xét số tự nhiên A hiện thời đang biểu diễn dưới dạng mũ hay một dạng nào đó mà ta không đếm được các chữ số của nó. Gỉ sử A có n chữ số thì ta có công thức sau đây: 
.
Trước khi đi vào chứng minh, tôi muốn nhắc lại cho các bạn cách phân tích một số tự nhiên ra dạng tổng lũy thừa của cơ số 10, ví dụ 
.
Chứng minh:
Giả sử số tự nhiên A có n chữ số:
Suy ra 
và
.
Từ hai điều này ta có: 
Giữa 
chỉ có duy nhất một số tự nhiên lớn hơn 
đó là 
Vậy 
Sau đây ta cùng sử dụng công thức trên để giải một số bài toán sau:
BÀI TOÁN ÁP DỤNG
Bài 1: Số nguyên tố dạng 
, trong đó p là một số nguyên tố, được gọi là số nguyên tố Mec-xen. Số 
được phát hiện năm 1999. Hỏi rằng nếu viết số đó trong hệ thập phân thì có bao nhiêu chữ số?
Trích đề thi thử Chuyên Hưng Yên lần 2.
A. 
chữ số. B. 2098961 chữ số.
C. 6972593 chữ số. D. 6972592 chữ số.
Giải:
Đầu tiên ta cần biết: Số tự nhiên A có n chữ số thì 
Ta cần tính 
có bao nhiêu chữ số, ta thấy rằng 
và 
chắc chắn có cùng số chữ số, nó giống như là 213 và 213−1 có cùng 3 chữ số vậy.
Từ lập luậ trên ta đi tính số chữ số của 
bằng công thức: 
. Áp dụng công thức ta được:
.
Chọn B.
Bài 2: Người ta qui ước 
và 
là giá trị của 
. Trong các lĩnh vực kỹ thuật, 
được sử dụng khá nhiều, kể cả máy tính cầm tay hay quang phổ. Hơn nữa, trong toán học người ta sử dụng 
để tìm số chữ số của một số nguyên dương nào đó. Ví dụ số A có n chữ số thì khi đó 
với 
là số nguyên lớn nhất nhỏ hơn hoặc bằng A. Hỏi số 
có bao nhiêu chữ số?
A. 9999 chữ số. B. 6666 chữ số. C. 9966 chữ số. D. 6699 chữ số.
Giải:
Áp dụng công thức 
để tìm các chữ số của số A.
Ta có: 
Vậy B có 6666 chữ số.
Chọn B.
Bài 3: Số nguyên tố dạng 
, trong đó p là số nguyên tố được gọi là số nguyên tố Mec-sen (Mersenne Marin, 1588-1648, người Pháp)
+ Ơ-le phát hiện 
năm 1750.
+ Luy-ca (Lucas Edouard, 1842-1891, người Pháp) phát hiện 
năm 1876
+ 
được phát hiện năm 1996.
Hỏi rằng nếu viết ba số đó trong hệ thập phân thì mỗ số có bao nhiêu chữ số?
A. 
B. 
C. 
D. 
Giải:
Giả sử số nguyên tố 
viết trong hệ thập phân có n chữ số thì 
hay 
vì 
không chứa thừa số nguyên tố 5 nên 
).
Suy ra: 
hay 
Thay 
, ta được 
Suy ra 
.
Vậy số nguyên tố 
viết trong hệ thập phân có 10 chữ số.
Làm tương tự ta thấy 
có 39 chữ số. số 
có 420921 chữ số.
Chọn A.
Bài 4: Số 
là một số nguyên tố. Hỏi nếu viết trong hệ thập phân thì số đó có bao nhiêu chữ số?
A. 227831 chữ số. B. 227832 chữ số. C. 227834 chữ số. D. 227835 chữ số.
Giải:
Áp dụng công thức 
để tìm các chữ số của số A.
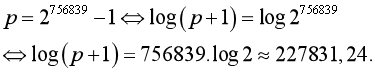
Vậy số p này có 227832 chữ số. chọn B.
Bài 5: Đầu năm 2016, Curtis Cooper và các công sự tại nhóm nghiên cứ Đại học Central Mis-souri, Mỹ vừa công bố số nguyên tố lớn nhất tại thời điểm đó. Số nguyên tố này là một dạng số Mersenne, có giá trị bằng 
. Hỏi 
có bao nhiêu chữ số?
A. 2233862 chữ số. B. 22338618 chữ số.
C. 22338617 chữ số. D. 2233863 chữ số.
Giải:
Áp dụng công thức 
để tìm các chữ số của số A.
Ta có: 
Do đó M có 22338617 chữ số.
Chọn B.
Bài 6: Nhà toán học người Pháp Pierre de Fermat là người đầu tiên đưa ra khai niệm số Fermat 
với n là số nguyên dương không âm. Fermat dự đoán 
là số nguyên tố, nhưng Euler đã chứng minh được 
là hợp số. Hãy tìm số chữ số của 
.
A. 1243 chữ số. B. 1234 chữ số. C. 2452 chữ số. D. 2467 chữ số.
Giải:
Ta có: 
.
Suy ra 
. Suy ra 
có 2467 chữ số. Chọn D.
CHỦ ĐỀ 2
CÁC DẠNG BÀI TOÁN LÃI SUẤT
1. Lãi đơn
Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.
Công thức tính lãi đơn: 
Trong đó:
: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
: Số tiền gửi ban đầu;
: Số kỳ hạn tính lãi;
: Lãi suất định kỳ, tính theo %.
2. Lãi kép
Là số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh ra thay đổi theo từng định kỳ.
a. Lãi kép, gửi một lần: 
Trong đó:
: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
: Số tiền gửi ban đầu;
: Số kỳ hạn tính lãi;
: Lãi suất định kỳ, tính theo %.
b. Lãi kép liên tục: 
Trong đó:
: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
: Số tiền gửi ban đầu;
: Số kỳ hạn tính lãi;
: Lãi suất định kỳ, tính theo %.
c. Lãi kép, gửi định kỳ.
Trường hợp gửi tiền định kì cuối tháng.
Bài toán 1: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép 
(tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?
Người ta chứng minh được số tiền thu được là:
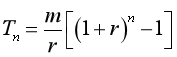
Chứng minh
|
Tháng |
Đầu tháng |
Cuối tháng |
|
1 |
Chưa gửi |
|
|
2 |
|
|
|
3 |
|
|
|
… |
… |
… |
|
|
|
Vậy sau tháng n ta được số tiền 
,
Ta thấy trong ngoặc là tổng 
số hạng của cấp số nhân có 
Ta biết rằng: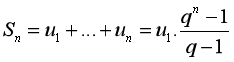 
nên 
Bài toán 2: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép 
(tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?
Người ta chứng minh được số tiền cần gửi mỗi tháng là: 
Chứng minh:
Áp dụng bài toán 1 ta có số tiền thu được là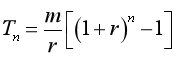 
, mà đề cho số tiền đó chính là A nên 
.
Bài toán 3: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép 
(tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?
Người ta chứng minh được số tháng thu được đề bài cho là: 
.
Chứng minh:
Áp dụng bài toán 1 ta có số tiền thu được là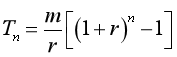 
, mà đề cho số tiền đó chính là A nên 
Như vậy trong trường hợp một này ta cần nắm vứng công thức Bài toán 1 từ đó có thể dễ dàng biến đổi ra các công thức ở bài toán 2, Bài toán 3.