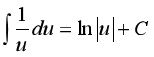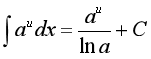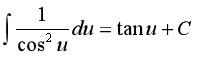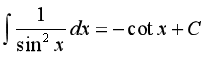BÀI TOÁN VẬN DỤNG CAO NGUYÊN HÀM, TÍCH PHÂN
CÁC BÀI TOÁN NGUYÊN HÀM
Đầu tiên xin nhắc lại các khái niệm và định lí căn bản để quý bạn đọc có kiến thức nền tảng trước khi đi vào các bài toán cụ thể.
1. Định nghĩa
Cho hàm số ![]() xác định trên tập K (khoảng, nửa khoảng, đoạn của R). Nếu Ta có hàm số
xác định trên tập K (khoảng, nửa khoảng, đoạn của R). Nếu Ta có hàm số ![]() xác định trên K sao cho
xác định trên K sao cho ![]() thì
thì ![]() được gọi là nguyên hàm của hàm số
được gọi là nguyên hàm của hàm số ![]() trên K.
trên K.
Định lí 1. Nếu ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên K thì với mỗi hằng số C, hàm số
trên K thì với mỗi hằng số C, hàm số ![]() cũng là một nguyên hàm của hàm số
cũng là một nguyên hàm của hàm số ![]() trên K.
trên K.
Định lí 2. Nếu ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên K thì mọi nguyên hàm của
trên K thì mọi nguyên hàm của ![]() trên K đều có dạng
trên K đều có dạng ![]() với C là hằng số.
với C là hằng số.
Định lí 3. Mọi hàm số ![]() liên tục trên K đều có nguyên hàm trên K.
liên tục trên K đều có nguyên hàm trên K.
2. Tính chất của nguyên hàm:
![]() với C là hằng số.
với C là hằng số.
![]() với k là hằng số khác 0.
với k là hằng số khác 0.
![]()
Bảng nguyên hàm
Chú ý: công thức tính vi phân của ![]() là
là ![]()
|
Với u là một hàm số |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Chúng ta sẽ cùng tìm hiểu một số bài toán Nguyên Hàm ở mức độ vận dụng sau đây:
BÀI TẬP VẬN DỤNG
Bài 1: Biết 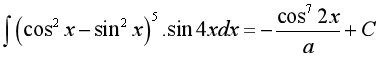 . Với a là số nguyên. Tìm a?
. Với a là số nguyên. Tìm a?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Giải:
Đặt ![]() , Ta có:
, Ta có:

Đặt ![]()
Vậy 
Chọn C.
Bài 2: Biết  . Với a là số nguyên. Tìm a?
. Với a là số nguyên. Tìm a?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Giải:
Vì  nên
nên
Nguyên hàm của:  là:
là: ![]() .
.
CHọn A.
Bài 3: Tìm một nguyên hàm của:  biết nguyên hàm này bằng 3 khi
biết nguyên hàm này bằng 3 khi  .
.
A.  B.
B.  C.
C. ![]() . D.
. D. ![]() .
.
Giải:

Nguyên hàm của ![]()
Ta có: 
Chọn C.
Bài 4: ![]() là nguyên hàm của:
là nguyên hàm của:
A. 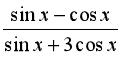 . B.
. B.  . C.
. C.  . D.
. D.  .
.
Giải:
Ta chỉ cần đạo hàm của F(x), rồi sau đó quan sát kết quả đúng.
Ta có: 
![]() là một nguyên hàm của
là một nguyên hàm của  .
.
Chọn D.
Bài 5: Biết  . Với a là số nguyên. Tìm a?
. Với a là số nguyên. Tìm a?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Giải:
Chú ý nếu chúng ta biến đổi:
 . Là sai
. Là sai
Điều sau đây mới đúng: 
Trở lại bài, ta sẽ biến đổi biểu thức ![]() về dạng
về dạng ![]() như sau:
như sau:

Chọn D.
CHỦ ĐỀ 2.
CÁC BÀI TOÁN TÍCH PHÂN.
1. Định nghĩa
Cho hàm số ![]() thỏa:
thỏa:
+ Liên tục trên đoạn ![]() .
.
+ ![]() là nguyên hàm của
là nguyên hàm của ![]() trên đoạn
trên đoạn ![]() .
.
Lúc đó hiệu số ![]() được gọi là tích phân từ a đến b và kí hiệu
được gọi là tích phân từ a đến b và kí hiệu 
Chú ý:
+ a, b được gọi là 2 cận của tích phân.
+ a = b thì 
+ a > b thì  .
.
+ Tích phân không phụ thuộc và biến số, tức là 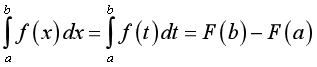 .
.
2. Tính chất của tích phân:
+ 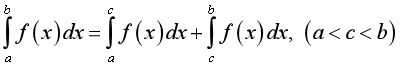 .
.
+ 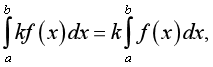 với k là hằng số khác 0.
với k là hằng số khác 0.
+ 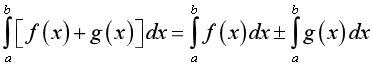 .
.
Chú ý:
Để tính tích phân từ a đến b, ta tiến hành tìm nguyên hàm rồi sau đó thay cận vào theo công thức 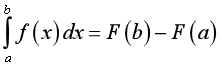 .
.
BÀI TẬP ÁP DỤNG
Một lần nữa xin nhắc lại rằng đây là cuốn sách đề cập đến các bài toán vận dụng và vận dụng cao nên trước khi sử dụng sách này quý bạn đọc cần có kiến thwucs cơ bản tốt. Bây giờ chúng ta cùng nghiên cứu các bài toán tích phân khá khó:
Bài 1: Nếu a là một số thỏa mãn các điều kiện sau:  và
và  thì:
thì:
A. ![]() B.
B. ![]() . C.
. C. ![]() D.
D. ![]() .
.
Giải:
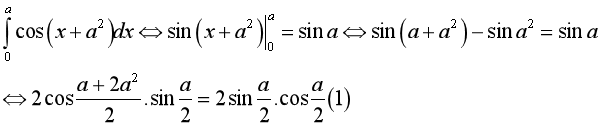
Vì  nên
nên 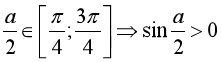 , vậy:
, vậy:
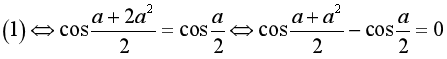
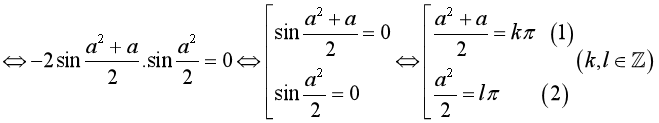 .
.
Vì ![]() nên (1) không thỏa mãn với mọi
nên (1) không thỏa mãn với mọi  ,hoặc thay 4 vào đáp án (1) ta thấy đều không thỏa.
,hoặc thay 4 vào đáp án (1) ta thấy đều không thỏa.
Đối với (2). Vì 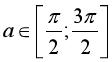 nên chọn l=1 lúc đó
nên chọn l=1 lúc đó ![]() .
.
Chọn D.
Bài 2: Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn điều kiện  . Khi đó:
. Khi đó:
A. ![]() B.
B. ![]() . C.
. C. ![]() D.
D. ![]() .
.
Giải:
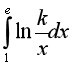
Dùng phương pháp tích phân từng phần


Vậy 
![]()
![]() mà k là số nguyên dương nên chọn
mà k là số nguyên dương nên chọn ![]() .
.
Chọn C.
Bài 3: Xét tích phân  . Bằng cách đặt
. Bằng cách đặt ![]() tích phân A được biến đổi thành tích phân nào sau đây.
tích phân A được biến đổi thành tích phân nào sau đây.
A.  . B.
. B.  . C.
. C.  . D.
. D.  .
.
Giải:
Ta có: 
![]()
Vậy:  , lúc này đặt
, lúc này đặt ![]() và đổi cận ta đc:
và đổi cận ta đc:
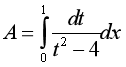 . Chọn A.
. Chọn A.
Bài 4: Đặt 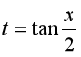 thì
thì  được biến đổi thành
được biến đổi thành  . Hãy xác định
. Hãy xác định ![]() :
:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Giải:

Đặt 
Vậy: 
Chọn B.
Bài 5: Biết  và
và  . Tính
. Tính 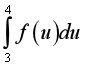 .
.
A. ![]() B.
B. ![]() C.
C. 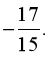 D.
D. ![]()
Giải:
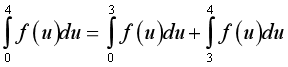 .
.
Mà  và
và 
Nên: 
Chọn D.
Chú ý: tích phân không phụ thuộc vào biến số.