CÁC PHÉP TOÁN TẬP HỢP

Vietlearn
26 minutes

I – LÝ THUYẾT

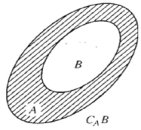
I – GIAO CỦA HAI TẬP HỢP

Tập hợp IMG_256 gồm các phần tử vừa thuộc IMG_257 vừa thuộc IMG_258 được gọi là giao của IMG_259 và IMG_260

IMG_261 Kí hiệu IMG_262 (phần gạch chéo trong hình).

Vậy IMG_263

IMG_264

II – HỢP CỦA HAI TẬP HỢP

Tập hợp IMG_265 gồm các phần tử thuộc IMG_266 hoặc thuộc IMG_267 được gọi là hợp của IMG_268 và IMG_269

IMG_270 Kí hiệu IMG_271 (phần gạch chéo trong hình).

Vậy IMG_272

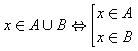
IMG_273

III – HIỆU VÀ PHẦN BÙ CỦA HAI TẬP HỢP

Tập hợp IMG_274 gồm các phần tử thuộc IMG_275 nhưng không thuộc IMG_276 gọi là hiệu của IMG_277 và IMG_278

IMG_279 Kí hiệu IMG_280

Vậy IMG_281

IMG_282

Khi IMG_283 thì IMG_284 gọi là phần bù của IMG_285 trong IMG_286 kí hiệu IMG_287

IMG_288


II – DẠNG TOÁN

1. Dạng 1: Xác định tập hợp bằng cách liệt kê

Phương pháp giải.

Chúng ta sẽ giải phương trình hoặc bất phương trình sau đó so sánh với điều kiện ban đầu của tập hợp.

A. VÍ DỤ MINH HỌA

Ví dụ 1: Liệt kê các phần tử của tập hợp IMG_289

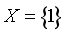  1. IMG_290 . B. IMG_291 . C. IMG_292 . D. IMG_293 .

Lời giải

Chọn A.

Cách 1: Giải phương trình IMG_294 . Hai nghiệm này đều thuộc IMG_295 .

Cách 2: Nhập vào máy tính IMG_296 sau đó ấn Calc lần lượt các đáp án, đáp án câu nào làm phương trình bằng 0 thì chọn đáp án đó.

Ví dụ 2: Liệt kê các phần tử của tập hợp IMG_297

  1. IMG_298 . B. IMG_299 . C. IMG_300 . D. IMG_301 .

Lời giải

Chọn C.

Cách 1: Giải bất phương trình IMG_302 Mà IMG_303 là các số tự nhiên nên chọn câu C.

Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.

Ví dụ 3: Liệt kê các phần tử của tập hợp 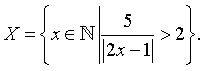IMG_304

  1. IMG_305 . B. IMG_306 . C. IMG_307 . D. IMG_308 .

Lời giải

Chọn B.

Cách 1: Giải bất phương trình 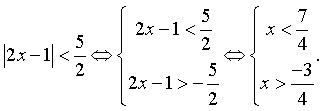IMG_309

Mà IMG_310 là các số tự nhiên nên chọn câu B.

Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.

Bức thư thứ 2 TÍN HIỆU ĐẦU TIÊN CỦA TUỔI DẬY THÌ

Ví dụ 4: Liệt kê các phần tử của tập hợp IMG_311

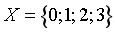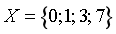  1. IMG_312 . B. IMG_313 .

C. IMG_314 D. IMG_315 .

Lời giải

Chọn D.

Cách 1: Giải phương trình IMG_316

Mà IMG_317 là các số nguyên nên chọn câu D.

Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.


B. BÀI TẬP TỰ LUYỆN

NHẬN BIẾT.

  1. Liệt kê các phần tử của tập hợp IMG_318

A. IMG_319 B. IMG_320 C. IMG_321 D. IMG_322

THÔNG HIỂU.

  1. Liệt kê các phần tử của tập hợp IMG_323

A. IMG_324 B. IMG_325 C. IMG_326 D. IMG_327

  1. Liệt kê các phần tử của tập hợp IMG_328

A. IMG_329 B. IMG_330 C. IMG_331 D. IMG_332


VẬN DỤNG.

  1. Liệt kê các phần tử của tập hợp IMG_333

A. IMG_334 B. IMG_335 C. IMG_336 D. IMG_337

C. ĐÁP ÁN PHẦN BÀI TẬP TỰ LUYỆN

Câu 1. A

Câu 2. B

Câu 3. B

Câu 4. C



2. Dạng 2: Xác định tập hợp bằng cách chỉ ra tính chất đặc trưng

Ví dụ 1: Tính chất đặc trưng của tập hợp IMG_338

A. IMG_339 B. IMG_340 C. IMG_341 D. IMG_342

Lời giải

Chọn A.

Ta liệt kê các phần tử từng đáp án, đáp án nào thỏa yêu cầu bài toán ta sẽ chọn.

Ví dụ 2: Tính chất đặc trưng của tập hợp IMG_343

A. IMG_344 B. IMG_345

C. IMG_346 D. IMG_347

Lời giải

Thế nào là bí mật “Tunguska”?
1 2 3 4 5 6 7