HÀM SỐ LIÊN TỤC

Vietlearn
5 minutes

A – LÝ THUYẾT VÀ PHƯƠNG PHÁP

1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x0 Û  IMG_256

· Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước:

B1: Tính f(x0).

B2: Tính IMG_257  (trong nhiều trường hợp ta cần tính IMG_258 , IMG_259 )

B3: So sánh IMG_260  với f(x0) và rút ra kết luận.

2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.

3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và

IMG_261

· Hàm số đa thức liên tục trên R.

· Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:

· Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0.

· Hàm số y = IMG_262  liên tục tại x0 nếu g(x0) ¹ 0.

4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c Î (a; b): f(c) = 0.

Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm cÎ (a; b).

Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = IMG_263 , M = IMG_264 . Khi đó với mọi T Î (m; M) luôn tồn tại ít nhất một số c Î (a; b): f(c) = T.

B – BÀI TẬP

DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM

Phương pháp:

IMG_265 Tìm giới hạn của hàm số IMG_266 khi IMG_267 và tính IMG_268

IMG_269 Nếu tồn tại IMG_270 thì ta so sánh IMG_271 với IMG_272 .

Chú ý:

1. Nếu hàm số liên tục tại IMG_273 thì trước hết hàm số phải xác định tại điểm đó

2. IMG_274 .

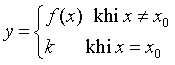3. Hàm số IMG_275 liên tục tại IMG_276 .

4. Hàm số IMG_277 liên tục tại điểm IMG_278 khi và chỉ khi IMG_279 .

Chú ý:

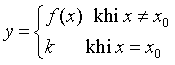IMG_280 Hàm số IMG_281 liên tục tại IMG_282 khi và chỉ khi

IMG_283 .

IMG_284 Hàm số IMG_285 liên tục tại IMG_286 khi và chỉ khi

IMG_287 .

Câu 1. Cho hàm số IMG_288 và IMG_289 với IMG_290 . Giá trị của IMG_291 để IMG_292 liên tục tại IMG_293 là:

A. IMG_294 . B. IMG_295 . C. IMG_296 . D. IMG_297

Câu 2. Cho hàm số IMG_298 . Chọn câu đúng trong các câu sau:

(I) IMG_299 liên tục tại IMG_300 .

(II) IMG_301 gián đoạn tại IMG_302 .

(III) IMG_303 liên tục trên đoạn IMG_304 .

Bướu cổ độc thể chìm

A. Chỉ IMG_305 và IMG_306 . B. Chỉ IMG_307 . C. Chỉ IMG_308 . D. Chỉ IMG_309 và IMG_310

Câu 3. Cho hàm số 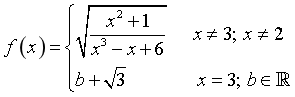IMG_311 . Tìm IMG_312 để IMG_313 liên tục tại IMG_314 .

A. IMG_315 . B. IMG_316 . C. IMG_317 . D. IMG_318

Câu 4. Cho hàm số IMG_319 . Tìm khẳng định đúng trong các khẳng định sau:

IMG_320 IMG_321 gián đoạn tại IMG_322

IMG_323 IMG_324 liên tục tại IMG_325

IMG_326 IMG_327

A. Chỉ IMG_328 . B. Chỉ IMG_329 . C. Chỉ IMG_330 và IMG_331 . D. Chỉ IMG_332 và IMG_333

Câu 5. Cho hàm số 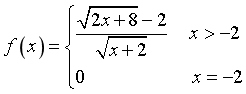IMG_334 . Tìm khẳng định đúng trong các khẳng định sau:

IMG_335 IMG_336 .

IMG_337 IMG_338 liên tục tại IMG_339

IMG_340 IMG_341 gián đoạn tại IMG_342

A. Chỉ IMG_343 và IMG_344 . B. Chỉ IMG_345 và IMG_346 . C. Chỉ IMG_347 . D. Chỉ IMG_348

Câu 6. Cho hàm số IMG_349 . Tìm khẳng định đúng trong các khẳng định sau:.

IMG_350 IMG_351 không xác định tại IMG_352

IMG_353 IMG_354 liên tục tại IMG_355

IMG_356 IMG_357

A. Chỉ IMG_358 . B. Chỉ IMG_359 và IMG_360 .

C. Chỉ IMG_361 và IMG_362 . D. Cả IMG_363 đều sai.

Câu 7. Cho hàm số 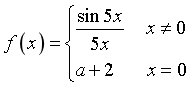IMG_364 . Tìm IMG_365 để IMG_366 liên tục tại IMG_367

A. IMG_368 . B. IMG_369 . C. IMG_370 . D. IMG_371

Câu 8.Cho hàm số IMG_372 . Tìm IMG_373 để IMG_374 gián đoạn tại IMG_375 .

A. IMG_376 . B. IMG_377 . C. IMG_378 . D. IMG_379 .

Câu 9.Cho hàm số IMG_380 . Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại IMG_381

B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại IMG_382

C. Hàm số không liên tục tại IMG_383

D. Tất cả đều sai

Câu 10. Cho hàm số IMG_384 . Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại IMG_385

B. Hàm số liên tục tại mọi điểm

C. Hàm số không liên tục tại IMG_386

D. Tất cả đều sai

Vì sao có động đất?