HOÁN VỊ, CHỈNH HỢP, TỔ HỢP

Vietlearn

11 minutes

A – LÝ THUYẾT TÓM TẮT

I. Hoán vị

1. Giai thừa:

Qui ước:

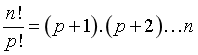(với )

2. Hoán vị (không lặp):

Một tập hợp gồm n phần tử (n ³ 1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n phần tử.

Số các hoán vị của n phần tử là:

3. Hoán vị lặp:

Cho k phần tử khác nhau: Một cách sắp xếp phần tử trong đó gồm phần tử phần tử phần tử theo một thứ tự nào đó được gọi là một hoán vị lặp cấp và kiểu của phần tử.

Số các hoán vị lặp cấp kiểu của phần tử là:

4. Hoán vị vòng quanh:

Cho tập A gồm n phần tử. Một cách sắp xếp n phần tử của tập A thành một dãy kín được gọi là một hoán vị vòng quanh của n phần tử.

Số các hoán vị vòng quanh của n phần tử là:

II. Chỉnh hợp

1. Chỉnh hợp (không lặp):

Cho tập hợp A gồm n phần tử. Mỗi cách sắp xếp k phần tử của A (1 £ k £ n) theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử của tập A.

Số chỉnh hợp chập k của n phần tử:

· Công thức trên cũng đúng cho trường hợp k = 0 hoặc k = n.

· Khi k = n thì

2. Chỉnh hợp lặp:

Cho tập A gồm n phần tử. Một dãy gồm k phần tử của A, trong đó mỗi phần tử có thể được lặp lại nhiều lần, được sắp xếp theo một thứ tự nhất định được gọi là một chỉnh hợp lặp chập k của n phần tử của tập A.

Số chỉnh hợp lặp chập k của n phần tử:

III. Tổ hợp

1. Tổ hợp (không lặp):

Cho tập A gồm n phần tử. Mỗi tập con gồm k (1 £ k £ n) phần tử của A được gọi là một tổ hợp chập k của n phần tử.

Số các tổ hợp chập k của n phần tử:

· Qui ước: = 1

Tính chất:

2. Tổ hợp lặp:

Cho tập A = và số tự nhiên k bất kì. Một tổ hợp lặp chập k của n phần tử là một hợp gồm k phần tử, trong đó mỗi phần tử là một trong n phần tử của A.

Số tổ hợp lặp chập k của n phần tử:

3. Phân biệt chỉnh hợp và tổ hợp:

· Chỉnh hợp và tổ hợp liên hệ nhau bởi công thức:

· Chỉnh hợp: có thứ tự.

· Tổ hợp: không có thứ tự.

Þ Những bài toán mà kết quả phụ thuộc vào vị trí các phần tử –> chỉnh hợp

Ngược lại, là tổ hợp.

· Cách lấy k phần tử từ tập n phần tử (k £ n):

+ Không thứ tự, không hoàn lại:

+ Có thứ tự, không hoàn lại:

+ Có thứ tự, có hoàn lại:

Phương án 2: Đếm gián tiếp (đếm phần bù)

Trong trường hợp hành động chia nhiều trường hợp thì ta đi đếm phần bù của bài toán như sau:

Đếm số phương án thực hiện hành động (không cần quan tâm đến có thỏa tính chất hay không) ta được phương án.

Đếm số phương án thực hiện hành động không thỏa tính chất ta được phương án.

Khi đó số phương án thỏa yêu cầu bài toán là: .

B – BÀI TẬP

DẠNG 1: BÀI TOÁN ĐẾM

Phương pháp: Dựa vào hai quy tắc cộng, quy tắc nhân và các khái niệm hoán vị, chỉnh hợp, tổ hợp.

Nước là gì?

Một số dấu hiệu giúp chúng ta nhận biết được hoán vị, chỉnh hợp hay tổ hợp.

1) Hoán vị: Các dấu hiệu đặc trưng để giúp ta nhận dạng một hoán vị của n phần tử là:

Tất cả n phần tử đều phải có mặt

Mỗi phần tử xuất hiện một lần.

Có thứ tự giữa các phần tử.

2) Chỉnh hợp: Ta sẽ sử dụng khái niệm chỉnh hợp khi

Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần

k phần tử đã cho được sắp xếp thứ tự.

3) Tổ hợp: Ta sử dụng khái niệm tổ hợp khi

Cần chọn phần tử từ n phần tử, mỗi phần tử xuất hiện một lần

Không quan tâm đến thứ tự k phần tử đã chọn.

Câu 1: Từ các số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?

A. 192 B. 202 C. 211 D. 180

Câu 2: Có 3 học sinh nữ và 2 hs nam.Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách sắp xếp để 3 học sinh nữ ngồi kề nhau

A. 34 B. 46 C. 36 D. 26

Câu 3: Có 3 học sinh nữ và 2 hs nam.Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách sắp xếp để 2 học sinh nam ngồi kề nhau.

A. 48 B. 42 C. 58 D. 28

Câu 4: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho A và F ngồi ở hai đầu ghế

A. 48 B. 42 C. 46 D. 50

Câu 5: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho:

A và F ngồi cạnh nhau

A. 242 B. 240 C. 244 D. 248

Câu 6: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho:

A và F không ngồi cạnh nhau

A. 480 B. 460 C. 246 D. 260

Câu 7: Trong tủ sách có tất cả cuốn sách. Hỏi có bao nhiêu cách sắp xếp sao cho quyển thứ nhất ở kề quyển thứ hai:

A. . B. . C. . D. .

Câu 8: Có bao nhiêu cách xếp sách Văn khác nhau và sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?

A. . B. . C. . D. .

Câu 9: Từ các số có thể lập được bao nhiêu số tự nhiên,mỗi số có 6 chữ số đồng thời thỏa điều kiện :sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.

A. 104 B. 106 C. 108 D. 112

Câu 10: Từ các số lập được bao nhiều số tự nhiên gôm chữ số thỏa mãn đồng thời hai điều kiện sau: Trong mỗi số, hai chữ số giống nhau không đứng cạnh nhau.

A. 76 B. 42 C. 80 D. 68

DẠNG 2: XẾP VỊ TRÍ – CÁCH CHỌN, PHÂN CÔNG CÔNG VIỆC..

Câu 1: Một liên đoàn bóng rổ có đội, mỗi đội đấu với mỗi đội khác hai lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là:

A. . B. . C. . D. .

Câu 2: Một liên đoàn bóng rổ có đội, mỗi đội đấu với mỗi đội khác hai lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là:

A. . B. . C. . D. .

Câu 3: Một liên đoàn bóng đá có đội, mỗi đội phải đá trận với mỗi đội khác, trận ở sân nhà và trận ở sân khách. Số trận đấu được sắp xếp là:

A. B. . C. . D. .

Câu 4: Giả sử ta dùng màu để tô cho nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:

A. . B. . C. . D. .

Câu 5: Sau bữa tiệc, mỗi người bắt tay một lần với mỗi người khác trong phòng. Có tất cả người lần lượt bắt tay. Hỏi trong phòng có bao nhiêu người: