PHƯƠNG TRÌNH ĐƯỜNG ELIP

I – LÝ THUYẾT

1)Định nghĩa: Cho hai điểm cố định với và hằng số Elip là tập hợp các điểm thỏa mãn .

Các điểm là tiêu điểm của Khoảng cách là tiêu cự của được gọi là bán kính qua tiêu.

2) Phương trình chính tắc của elip:

Với :

trong đó

(1) được gọi là phương trình chính tắc của

3) Hình dạng và tính chất của elip:

Elip có phương trình (1) nhận các trục tọa độ là trục đối xứng và gốc tọa độ làm tâm đối xứng.

+ Tiêu điểm: Tiêu điểm trái tiêu điểm phải

+ Các đỉnh :

+ Trục lớn : , nằm trên trục trục nhỏ : , nằm trên trục

+ Hình chữ nhật tạo bởi các đường thẳng gọi là hình chữ nhật cơ sở.

+ Tâm sai :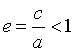

+ Bán kính qua tiêu điểm của điểm thuộc là:

II – DẠNG TOÁN

1. Dạng 1: Xác định độ dài các trục khi cho sẵn phương trình elip.

a) Phương pháp giải tự luận.

Từ phương trình chính tắc của ta có thể xác định được:

+ Các đỉnh :

+ Trục lớn : trục nhỏ :

Ví dụ: Cho elip có phương trình: Khi đó độ dài trục lớn, trục nhỏ lần lượt là.

A. B. C. D.

Lời giải

Ta có:

– Trục lớn:

– Trục nhỏ:

Chọn B

b) Phương pháp giải trắc nghiệm, casio.

2. Dạng 2: Xác định tọa độ các tiêu điểm khi cho sẵn phương trình elip.

a) Phương pháp giải tự luận.

Từ phương trình chính tắc của ta có thể xác định được:

+ Các đỉnh :

+ Tiêu điểm: Tiêu điểm trái tiêu điểm phải với

Ví dụ: Cho elip có phương trình: Khi đó tọa độ tiêu điểm của elip là.

A. B.

C. D.

Lời giải

Ta có:

– Tiêu điểm là:

Chọn A

b) Phương pháp giải trắc nghiệm, casio.

3. Dạng 3: Xác định tọa độ các tiêu điểm khi cho sẵn phương trình elip.

a) Phương pháp giải tự luận.

Từ phương trình chính tắc của 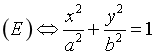ta có thể xác định được:

+ Các đỉnh :

Ví dụ 1: Cho elip có phương trình: Khi đó tọa độ hai đỉnh trên trục lớn của elip là.

A. B.

C. D.

Lời giải

Ta có:

– Hai đỉnh trên trục lớn là:

Chọn D

Ví dụ 2: Cho elip có phương trình: 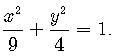Khi đó tọa độ hai đỉnh trên trục nhỏ của elip là.

A. B.

C. D.

Lời giải

Ta có:

– Hai đỉnh trên trục lớn là:

Chọn A

b) Phương pháp giải trắc nghiệm, casio.

4. Dạng 4: Lập phương trình chính tắc của elip khi biết độ dài trục lớn và trục nhỏ.

a) Phương pháp giải tự luận.

+ Trục lớn : trục nhỏ : Ta xác định được

+ Viết phương trình elip: