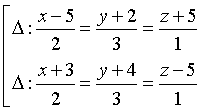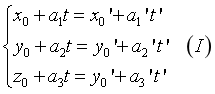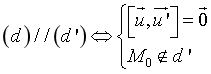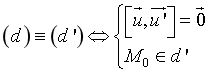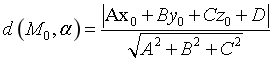PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO
A – LÝ THUYẾT CHUNG
1. Định nghĩa
Phương trình tham số của đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vec tơ chỉ phương
và có vec tơ chỉ phương ![]() :
: 
Nếu ![]() đều khác không. Phương trình đường thẳng
đều khác không. Phương trình đường thẳng ![]() viết dưới dạng chính tắc như sau:
viết dưới dạng chính tắc như sau:
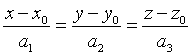
Ngoài ra đường thẳng còn có dạng tổng quát là: 
với ![]() thỏa
thỏa ![]()
2. Vị trí tương đối của hai đường thẳng
|
Chương trình cơ bản |
Chương trình nâng cao |
|
1 )Vị trí tương đối của hai đường thẳng Trong không gian
Vtcp ·
·
· d chéo d’ · d cắt d’ |
1 ) Vị trí tương đối của hai đường thẳng Trong không gian
Vtcp · · · · |
3. Vị trí tương đối của đường thẳng và mặt phẳng
|
Phương pháp 1 |
Phương pháp 2 |
|
Trong không gian
Pt: · Phương trình · Phương trình · Phương trình Đặc biệt: |
Trong không gian · · · |
4. Khoảng cách
|
Khoảng cách từ |
|
|
Khoảng cách từ M đến đường thẳng Phương pháp 1: · Lập ptmp · Tìm tọa độ giao điểm · Ø Khoảng cách giữa hai đường thẳng chéo nhau Phương pháp 1:
Lập phương trình mp |
Ø Khoảng cách từ M đến đường thẳng Phương pháp 2: (
Ø Khoảng cách giữa hai đường thẳng chéo nhau Phương pháp 2:
|
5. Góc giữa hai đường thẳng
Ø Góc giữa hai đường thẳng
![]() đi qua
đi qua ![]() có VTCP
có VTCP ![]()
![]() đi qua
đi qua ![]() có VTCP
có VTCP ![]()

6. Góc giữa đường thẳng và mặt phẳng
Góc giữa đường thẳng và mặt phẳng ![]() đi qua
đi qua ![]() có VTCP
có VTCP ![]() , mặt phẳng
, mặt phẳng ![]() có VTPT
có VTPT ![]()
Gọi ![]() là góc hợp bởi
là góc hợp bởi ![]() và mặt phẳng
và mặt phẳng 
B – CÁC DẠNG TOÁN VỀ PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Để lập phương trình đường thẳng ![]() ta cần xác định một điểm thuộc
ta cần xác định một điểm thuộc ![]() và một VTCP của nó.
và một VTCP của nó.
Dạng 1. Viết phương trình đường thẳng ![]() đi qua
đi qua ![]() và có vtcp
và có vtcp ![]() :
:
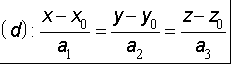
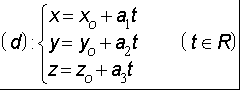
hoặc
Dạng 2. Đường thẳng ![]() đi qua
đi qua ![]() và
và ![]() :
:
· Đường thẳng ![]() đi qua
đi qua ![]() (hoặc
(hoặc ![]() ) có vtcp
) có vtcp ![]()
· Sử dụng dạng 1 để viết phương trình đường thẳng ![]() .
.
Dạng 3. Đường thẳng ![]() qua
qua ![]() và song song
và song song ![]()
· Đường thẳng ![]() đi qua
đi qua ![]() và có vtcp
và có vtcp ![]()
· Sử dụng dạng 1 để viết phương trình đường thẳng ![]() .
.
Dạng 4. Đường thẳng ![]() qua
qua ![]() và vuông góc mp
và vuông góc mp ![]()
· Đường thẳng ![]() đi qua
đi qua ![]() và có vtcp
và có vtcp ![]()
· Sử dụng dạng 1 để viết phương trình đường thẳng ![]() .
.
Dạng 5. Đường thẳng ![]() qua
qua ![]() và vuông góc 2 đường thẳng
và vuông góc 2 đường thẳng ![]() và
và ![]() :
:
· Đường thẳng ![]() đi qua
đi qua ![]() và có vtcp
và có vtcp ![]()
· Sử dụng dạng 1 để viết phương trình đường thẳng ![]() .
.
Dạng 6. Đường thẳng ![]() là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng ![]() :
:
· Cách 1: Tìm một điểm và một vtcp.
– Tìm toạ độ một điểm ![]() Î
Î ![]() : Bằng cách giải hệ phương trình
: Bằng cách giải hệ phương trình ![]()
(với việc chọn giá trị cho một ẩn ta sẽ giải hệ tìm giá trị hai ẩn còn lại)
– Tìm một vtcp của ![]() :
: ![]()
· Cách 2: Tìm hai điểm ![]() thuộc
thuộc ![]() , rồi viết phương trình đường thẳng đi qua hai điểm đó.
, rồi viết phương trình đường thẳng đi qua hai điểm đó.
Dạng 7. Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và vuông góc với hai đường thẳng
và vuông góc với hai đường thẳng ![]() :
:
· Vì ![]() ^
^ ![]() ,
, ![]() ^
^ ![]() nên một vtcp của
nên một vtcp của ![]() là:
là: ![]()
· Sử dụng dạng 1 để viết phương trình đường thẳng ![]() .
.
Dạng 8. Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() , vuông góc và cắt đường thẳng
, vuông góc và cắt đường thẳng ![]() .
.
· Cách 1: Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên đường thẳng D
trên đường thẳng D
Ta có 
![]()
Khi đó đường thẳng ![]() là đường thẳng đi qua
là đường thẳng đi qua ![]() (trở về dạng 2).
(trở về dạng 2).
· Cách 2: Gọi ![]() là mặt phẳng đi qua
là mặt phẳng đi qua ![]() và vuông góc với
và vuông góc với ![]() ;
; ![]() là mặt phẳng đi qua
là mặt phẳng đi qua ![]() và chứa
và chứa
![]() . Khi đó
. Khi đó ![]()
![]() (trở về dạng 6).
(trở về dạng 6).
· Cách 3: Gọi ![]() là mặt phẳng đi qua
là mặt phẳng đi qua ![]() và vuông góc với
và vuông góc với ![]()
– Tìm điểm ![]()
– Viết phương trình đường thẳng ![]() đi qua hai điểm
đi qua hai điểm ![]() (quay về dạng 2).
(quay về dạng 2).
Dạng 9. Đường thẳng ![]() nằm trong mặt phẳng
nằm trong mặt phẳng ![]() , vuông góc và cắt đường thẳng
, vuông góc và cắt đường thẳng ![]()
· Tìm giao điểm ![]() của
của ![]() và
và ![]()
![]()
· Vì 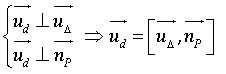
Dạng 10. Đường thẳng ![]() qua
qua ![]() và cắt
và cắt ![]() :
:
· ![]() với mp
với mp ![]() chứa
chứa ![]() và
và ![]() ; mp
; mp ![]() chứa
chứa ![]() và
và ![]() (trở về dạng 6)
(trở về dạng 6)
Dạng 11. Đường thẳng ![]() nằm trong mặt phẳng
nằm trong mặt phẳng ![]() và cắt cả hai đường thẳng
và cắt cả hai đường thẳng ![]() :
:
· Tìm các giao điểm ![]() Khi đó
Khi đó ![]() chính là đường thẳng
chính là đường thẳng ![]() (về dạng 2).
(về dạng 2).
Dạng 12. Đường thẳng ![]() và cắt
và cắt ![]() :
:
· Viết phương trình mặt phẳng ![]() chứa
chứa ![]() và
và ![]() , mặt phẳng
, mặt phẳng ![]() chứa
chứa ![]() và
và ![]()
Khi đó ![]()
![]() (trở về dạng 6).
(trở về dạng 6).
Dạng 13. Đường thẳng ![]() qua
qua ![]() và
và ![]()
![]() , cắt
, cắt ![]() :
:
· Cách 1:
– Viết phương trình mp ![]() qua
qua ![]() và vuông góc với
và vuông góc với ![]()
– Tìm ![]()
– Khi đó ![]() chính là đường thẳng AB (về dạng 2).
chính là đường thẳng AB (về dạng 2).
· Cách 2:
– Viết phương trình mặt phẳng ![]() qua
qua ![]() và vuông góc với
và vuông góc với ![]()
– Viết phương trình mặt phẳng ![]() chứa
chứa ![]() và
và ![]()
– Khi đó ![]()
![]() . (trở về dạng 6)
. (trở về dạng 6)
· Cách 3:
– Viết phương trình tham số ![]() của đường thẳng
của đường thẳng ![]() (nếu chưa có).
(nếu chưa có).
– Tìm điểm ![]() (
( ![]() có tọa độ theo tham số
có tọa độ theo tham số ![]() ) thỏa mãn
) thỏa mãn ![]()
Giải phương trình tìm được ![]()
– Viết phương trình đường thẳng ![]() đi qua hai điểm
đi qua hai điểm ![]() .
.
Dạng 14. Đường thẳng ![]() cắt
cắt ![]() :
:
· Tìm mp ![]() chứa
chứa ![]() chứa
chứa ![]()
· ![]() (trở về dạng 6).
(trở về dạng 6).
Dạng 15. Đường thẳng ![]() là hình chiếu của
là hình chiếu của ![]() lên
lên ![]() :
:
· Cách 1:
– Viết phương trình mặt phẳng ![]() chứa
chứa ![]() và vuông góc với
và vuông góc với ![]() .
.
– Đường thẳng ![]() là giao tuyến của
là giao tuyến của ![]() và
và ![]() (trở về dạng 6).
(trở về dạng 6).
· Cách 2:
– Xác định ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() .
.
– Lấy điểm ![]() trên
trên ![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() đi qua
đi qua ![]() vuông góc với
vuông góc với ![]() .
.
– Tìm tọa độ điểm ![]() là giao điểm của
là giao điểm của ![]() với
với ![]() .
.
– Đường thẳng ![]() chính là đường thẳng
chính là đường thẳng ![]() (trở về dạng 2).
(trở về dạng 2).
Đặc biệt: Nếu ![]() song song
song song ![]() thì
thì ![]() là đường thẳng đi qua
là đường thẳng đi qua ![]() và song song với
và song song với ![]() .
.
Dạng 16. Phương trình đường vuông góc chung của hai đường thẳng chéo nhau ![]() và
và ![]() :
:
· Cách 1:
– Chuyển phương trình đường thẳng ![]() về dạng tham số và xác định
về dạng tham số và xác định ![]() lần lượt là vtcp của
lần lượt là vtcp của ![]() .
.
– Lấy ![]() lần lượt thuộc
lần lượt thuộc ![]() (tọa độ
(tọa độ ![]() phụ thuộc vào tham số).
phụ thuộc vào tham số).
– Giả sử ![]() là đường vuông góc chung. Khi đó:
là đường vuông góc chung. Khi đó: 

Giải hệ phương trình ![]() tìm ra giá trị của tham số. Từ đó tìm được
tìm ra giá trị của tham số. Từ đó tìm được ![]() .
.
– Viết phương trình đường vuông góc chung ![]() .
.
· Cách 2:
– Vì d ^ d1 và d ^ d2 nên một vtcp của ![]() là:
là: ![]()
– Lập phương trình mặt phẳng ![]() chứa 2 đường thẳng cắt nhau
chứa 2 đường thẳng cắt nhau ![]() và
và ![]() , bằng cách:
, bằng cách:
+ Lấy một điểm ![]() trên
trên ![]() .
.
+ Một vtpt của ![]() là:
là: ![]()
– Tương tự lập phương trình mặt phẳng ![]() chứa 2 đường thẳng cắt nhau
chứa 2 đường thẳng cắt nhau ![]() và
và ![]() .
.
Khi đó ![]()
![]() (trở về dạng 6).
(trở về dạng 6).
· Cách 3:
– Vì ![]() và
và ![]() nên một vtcp của
nên một vtcp của ![]() là:
là: ![]()
– Lập phương trình mặt phẳng ![]() chứa 2 đường thẳng cắt nhau
chứa 2 đường thẳng cắt nhau ![]() và
và ![]() , bằng cách:
, bằng cách:
+ Lấy một điểm ![]() trên
trên ![]() .
.
+ Một vtpt của ![]() là:
là: ![]()
– Tìm ![]() . Khi đó viết phương trình
. Khi đó viết phương trình ![]() qua
qua ![]() có vtcp
có vtcp ![]() .
.
CÁC DẠNG TOÁN KHÁC
Dạng 1. Tìm ![]() là hình chiếu của
là hình chiếu của ![]() trên đường thẳng
trên đường thẳng ![]()
· Cách 1:
– Viết phương trình mp ![]() qua
qua ![]() và vuông góc với
và vuông góc với ![]() : ta có
: ta có ![]()
– Khi đó: ![]()
![]() tọa độ
tọa độ ![]() là nghiệm của hpt:
là nghiệm của hpt: ![]() và
và ![]() .
.
· Cách 2:
– Đưa ![]() về dạng tham số. Điểm
về dạng tham số. Điểm ![]() được xác định bởi:
được xác định bởi: 
Dạng 2. Điểm ![]() đối xứng với
đối xứng với ![]() qua đường thẳng
qua đường thẳng ![]() :
:
· Cách 1:
– Tìm hình chiếu ![]() của
của ![]() trên
trên ![]()
– Xác định điểm ![]() sao cho
sao cho ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() (công thức trung điếm).
(công thức trung điếm).
· Cách 2:
– Gọi ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() . Tính toạ độ điểm
. Tính toạ độ điểm ![]() theo toạ độ của
theo toạ độ của ![]() (công thức trung điếm).
(công thức trung điếm).
– Khi đó toạ độ của điểm ![]() được xác định bởi:
được xác định bởi:  .
.
Dạng 3. Đường thẳng ![]() đối xứng đường thẳng
đối xứng đường thẳng ![]() qua mặt phẳng
qua mặt phẳng ![]()
· TH1: ![]()
![]()
![]()
![]()
– Xác định ![]() là giao điểm của
là giao điểm của ![]() và
và ![]()
– Lấy điểm ![]() (
( ![]() bất kỳ). Tìm tọa độ điểm
bất kỳ). Tìm tọa độ điểm ![]() đối xứng với
đối xứng với ![]() qua
qua ![]() .
.
– Đường thẳng ![]() chính là đường thẳng
chính là đường thẳng ![]() .
.
· TH2: ![]()
![]()
![]()
– Lấy điểm ![]() (
( ![]() bất kỳ). Tìm tọa độ điểm
bất kỳ). Tìm tọa độ điểm ![]() đối xứng với
đối xứng với ![]() qua
qua ![]() .
.
– Đường thẳng ![]() chính là đường thẳng qua
chính là đường thẳng qua ![]() và song song
và song song ![]() .
.
C – BÀI TẬP TRẮC NGHIỆM
Câu 1: Đường thẳng ![]() song song với
song song với  và cắt cả hai đường thẳng
và cắt cả hai đường thẳng 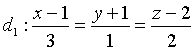 và
và  . Phương trình nào không phải đường thẳng
. Phương trình nào không phải đường thẳng ![]()
A. 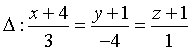 B.
B. 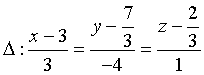
C.  D.
D. 
Câu 2: Cho đường thẳng  và mp (P) :
và mp (P) : ![]() . Tìm phương trình đường thẳng nằm trong mặt phẳng (P) cắt và vuông góc với (d).
. Tìm phương trình đường thẳng nằm trong mặt phẳng (P) cắt và vuông góc với (d).
A.  B.
B.  C.
C.  D.
D. 
Câu 3: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  và mặt phẳng
và mặt phẳng ![]() Phương trình đường thẳng
Phương trình đường thẳng ![]() nằm trong
nằm trong ![]() sao cho
sao cho ![]() cắt và vuông góc với đường thẳng
cắt và vuông góc với đường thẳng ![]() là
là
A. 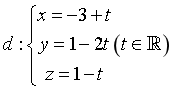 . B.
. B.  .
.
C.  . D.
. D.  .
.
Câu 4: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  và mặt phẳng
và mặt phẳng ![]() Viết phương trình đường thẳng
Viết phương trình đường thẳng ![]() nằm trong
nằm trong ![]() sao cho
sao cho ![]() vuông góc với
vuông góc với ![]() và khoảng cách giữa hai đường thẳng
và khoảng cách giữa hai đường thẳng ![]() và
và ![]() bằng
bằng ![]()
A.  . B.
. B.  .
.
C. 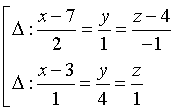 . D.
. D. 
Câu 5: Cho hai điểm ![]() và mặt phẳng
và mặt phẳng ![]() . Đường thẳng
. Đường thẳng ![]() nằm trên
nằm trên ![]() sao cho mọi điểm của
sao cho mọi điểm của ![]() cách đều 2 điểm
cách đều 2 điểm ![]() có phương trình là
có phương trình là
A.  B.
B.  C.
C. 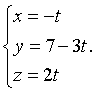 D.
D. 
Câu 6: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  và mặt phẳng
và mặt phẳng ![]() Gọi
Gọi ![]() là giao điểm của
là giao điểm của ![]() Tìm
Tìm ![]() sao cho
sao cho ![]() vuông góc với
vuông góc với ![]() và
và ![]()
A. 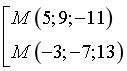 . B.
. B.  .
.
C. 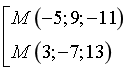 . D.
. D.  .
.
Câu 7: Trong không gian ![]() cho hai mặt phẳng
cho hai mặt phẳng ![]() Viết phương trình của đường thẳng
Viết phương trình của đường thẳng ![]() đi qua
đi qua ![]() nằm trong mặt phẳng
nằm trong mặt phẳng ![]() và tạo với mặt phẳng
và tạo với mặt phẳng ![]() một góc bằng
một góc bằng ![]()
A. 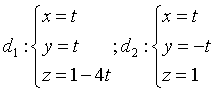 . B.
. B. 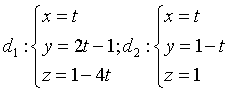 .
.
C. 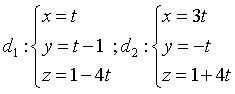 . D.
. D. 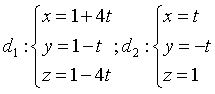
Câu 8: Trong không gian với hệ tọa độ ![]() cho hình thang cân
cho hình thang cân ![]() có hai đáy
có hai đáy ![]() thỏa mãn
thỏa mãn ![]() và diện tích bằng 27; đỉnh
và diện tích bằng 27; đỉnh ![]() phương trình đường thẳng chứa cạnh
phương trình đường thẳng chứa cạnh ![]() là
là 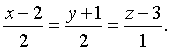 Tìm tọa độ các điểm
Tìm tọa độ các điểm ![]() biết hoành độ điểm
biết hoành độ điểm ![]() lớn hơn hoành độ điểm
lớn hơn hoành độ điểm ![]()
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]()
Câu 9: Trong không gian với hệ tọa độ ![]() cho hai đường thẳng
cho hai đường thẳng 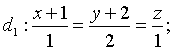
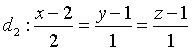 và mặt phẳng
và mặt phẳng ![]() Lập phương trình đường thẳng d song song với mặt phẳng
Lập phương trình đường thẳng d song song với mặt phẳng ![]() và cắt
và cắt ![]() lần lượt tại
lần lượt tại ![]() sao cho độ dài đoạn
sao cho độ dài đoạn ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
A. 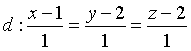 . B.
. B.  .
.
C.  . D.
. D. 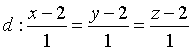
Câu 10: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  và mặt phẳng
và mặt phẳng ![]() Gọi
Gọi ![]() là giao điểm giữa
là giao điểm giữa ![]() và
và ![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() nằm trong mặt phẳng
nằm trong mặt phẳng ![]() , vuông góc với
, vuông góc với ![]() đồng thời khoảng cách từ
đồng thời khoảng cách từ ![]() đến
đến ![]() bằng
bằng ![]()
A. 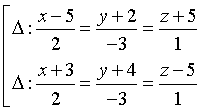 . B.
. B.  .
.
C. 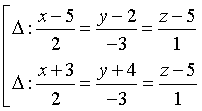 . D.
. D.