PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN VÀ PHƯƠNG TRÌNH BẬC NHẤT VỚI MỘT HÀM SỐ LƯỢNG GIÁC

1. Phương trình sinx = sina

a)

b)

c)

d)

e)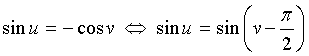

 

Các trường hợp đặc biệt:

 

2. Phương trình cosx = cosa

a)

b)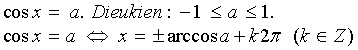

c)

d)

e)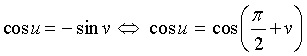

Các trường hợp đặc biệt:

 

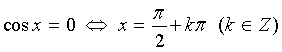
3. Phương trình tanx = tana

a)

b)

c)

d)

e)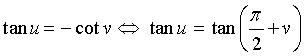

Các trường hợp đặc biệt:

 

4. Phương trình cotx = cota

Các trường hợp đặc biệt:

5. Phương trình bậc nhất đối với một hàm số lượng giác

Có dạng với với là một hàm số lượng giác nào đó

Cách giải: đưa về phương trình lượng giác cơ bản

6. Một số điều cần chú ý:

a) Khi giải phương trình có chứa các hàm số tang, cotang, có mẫu số hoặc chứa căn bậc chẵn, thì nhất thiết phải đặt điều kiện để phương trình xác định.

* Phương trình chứa tanx thì điều kiện:

* Phương trình chứa cotx thì điều kiện:

* Phương trình chứa cả tanx và cotx thì điều kiện

* Phương trình có mẫu số:

·

·

·

·

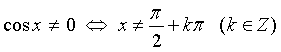
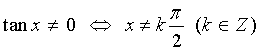
b) Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng một trong các cách sau để kiểm tra điều kiện:

1. Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.

2. Dùng đường tròn lượng giác để biểu diễn nghiệm

3. Giải các phương trình vô định.

c) Sử dụng MTCT để thử lại các đáp án trắc nghiệm