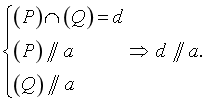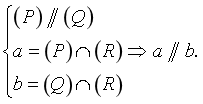A – LÝ THUYẾT CHUNG

I – ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Mở đầu về hình học không gian

Hình học không gian có các đối tượng cơ bản là điểm, đường thẳng và mặt phẳng.

Quan hệ thuộc: Trong không gian:

1. Với một điểm 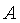và một đường thẳng có thể xảy ra hai trường hợp:

Điểm thuộc đường thẳng , kí hiệu

Điểm không thuộc đường thẳng, kí hiệu

b. Với một điểm và một mặt phẳng có thể xảy ra hai trường hợp:

Điểm thuộc mặt thẳng , kí hiệu

Điểm không thuộc đường thẳng, kí hiệu

2. Các tính chất thừa nhận của hình học không gian

Tính chất thừa nhận 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Tính chất thừa nhận 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

Tính chất thừa nhận 3: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

Tính chất thừa nhận 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Tính chất thừa nhận 5: Trong mỗi mặt phẳng, các kết đã biết của hình học phẳng đều đúng.

Định lí: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

3. Điều kiện xác định mặt phẳng

Có bốn cách xác định trong một mặt phẳng:

Cách 1: Một mặt phẳng được xác định nếu biết nó đi qua ba điểm không thẳng hàng của mặt phẳng, kí hiệu

Cách 2: Một mặt phẳng được xác định nếu biết nó đi qua một đường thẳng và một điểm không thuộc kí hiệu

Cách 3: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng cắt nhau, kí hiệu

Cách 4: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng song song, kí hiệu

4. Hình chóp và tứ diện

Định nghĩa: Cho đa giác và cho điểm nằm ngoài mặt phẳng chứa đa giác đó. Nối với các đỉnh ta được miền đa giác

Hình gồm tam giác đó và đa giác được gọi là hình chóp

Trong đó:

Điểm  gọi là đỉnh của hình chóp. Đa giác  gọi là mặt đáy của hình chóp. Các đoạn thẳng  gọi là các cạnh đáy của hình chóp. Các đoạn thẳng  gọi là các cạnh bên của hình chóp. Các miền tam giác  gọi là các mặt bên của hình chóp.

Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…

Chú ý

a. Hình chóp tam giác còn được gọi là hình tứ diện.

b. Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.

II – ĐƯỜNG THẲNG SONG SONG VỚI ĐƯỜNG THẲNG

1. Định nghĩa

Trong phần vị trí tương đối của hai đường thẳng trong không gian, ta biết rằng hai đường thẳng phân biệt bất kì hoặc chéo nhau hoặc song song hoặc cắt nhau. Nếu hai đường thẳng phân biệt đồng phẳng và không cắt nhau thì ta nói hai đường thẳng đó song song với nhau.

Định nghĩa:

Hai đường thẳng phân biệt trong không gian được gọi là song song với nhau, kí hiệu nếu chúng đồng phẳng và không cắt nhau.

2. Tính chất

Định lí 1: Trong không gian cho đường thẳng và điểm nằm ngoài . Lúc đó tồn tại duy nhất một đường thẳng và và song song với đường thẳng d.

Chú ý:

Định lí này cho ta thêm một cách xác định đường thẳng trong không gian: đó là đường thẳng đi qua một điểm và song song với một đường thẳng cho trước không chứa điểm đó. Kết hợp với định lí 2 dưới đây cho ta một cách để xác định giao tuyến của hai mặt phẳng.

Định lí 2 ( Về giao tuyến của ba mặt phẳng):

Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

Hệ quả:

Nếu hai mặt phẳng phân biệt chứa hai đường thẳng song song thì giao tuyến của chúng ( nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Đến đây ta có thể bổ sung một phương pháp tìm giao tuyến của hai mặt phẳng:

Bước 1: Chỉ ra hai mặt phẳng lần lượt chứa hai đường thẳng song song .

Bước 2: Tìm một điểm chung của hai mặt phẳng

Bước 3: Khi đó

Định lí 3:

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

Như vậy, cho hai đường thẳng phân biệt thỏa mãn

3. Góc giữa hai đường thẳng trong không gian

a) Định nghĩa

Góc giữa hai đường thẳng và trong không là góc giữa hai đường thẳng và cùng đi

qua một điểm và lần lượt song song với và .

b. Phương pháp tính góc giữa hai đường thẳng trong không gian

Bước 1: Dựng góc

– Tìm trên hình vẽ xem góc giữa hai đường thẳng có sẵn không?

– Nếu không có sẵn thì ta tiến hành:

+ Chọn một điểm O bất kì trong không gian.

+ Qua O dựng đường thẳng . Góc nhọn hay góc vuông tọc bởi chính là góc giữa và .

Lưu ý:

+ Ta thường lấy điểm O thuộc một trong hai đường thẳng và .

+ Chọn O sao cho góc giữa là góc của một tam giác mà độ dài các cạnh của nó đã biết hoặc có thể tính dễ dàng

Bước 2: Tính góc

Dùng hệ thức lượng trong tam giác, tỉ số lượng giác hay định lí cosin, sin. Trường hợp góc giữa hai đường thẳng và bằng ta nói .

III – ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

1. Vị trí tương đối của đường thẳng và mặt phẳng

Cho đường thẳng và mặt phẳng Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:

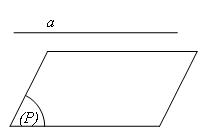
a. Đường thẳng và mặt phẳng không có điểm chung, tức là:

b. Đường thẳng và mặt phẳng chỉ có một điểm chung, tức là:

cắt tại

c. Đường thẳng và mặt phẳng có hai điểm chung, tức là:

cắt

2. Điều kiện để một đường thẳng song song với một mặt phẳng

Định lí 1: Nếu đường thẳng  không nằm trong mặt phẳng  và song song với một đường thẳng nào đó trong  thì  song song với Tức là,  thì nếu:

3. Tính chất

Định lí 2: Nếu đường thẳng  song song với mặt phẳng  thì mọi mặt phẳng  chứa  mà cắt  thì sẽ cắt theo một giao tuyến song song với Tức là, nếu

Hệ quả 1: Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng.

Hệ quả 2: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến (nếu có) của chúng song song với đường thẳng đó. Tức là:

Hệ quả 3: Nếu và là hai đường thẳng chéo nhau thì qua có một và chỉ một mặt phẳng song song với

IV – HAI MẶT PHẲNG SONG SONG

1. Vị trí tương đối của hai mặt phẳng phân biệt

Cho 2 mặt phẳng và Căn cứ vào số đường thẳng chung của 2 mặt phẳng ta có ba trường hợp sau:

a. Hai mặt phẳng và không có đường thẳng chung, tức là:

b. Hai mặt phẳng và chỉ có một đường thẳng chung, tức là:

cắt

c. Hai mặt phẳng và có 2 đường thẳng chung phân biệt, tức là:

cắt

2. Điều kiện để hai mặt phẳng song song

Định lí 1: Nếu mặt phẳng chứa hai đường thẳng cắt nhau và cùng song song với

mặt phẳng  thì  song song Tức là:

3. Tính chất

Tính chất 1: Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó.

Hệ quả 1: Nếu đường thẳng song song với mặt phẳng thì qua có một và chỉ một mặt phẳng song song với

Hệ quả 2: Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau. Tính chất 2: Nếu hai mặt phẳng  và  song song thì mặt phẳng  đã cắt  thì phải cắt  và các giao tuyến của chúng song song. Tức là:
Định lí Ta – lét trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỷ lệ. Tức là:

4. Hình lăng trụ và hình hộp

Định nghĩa hình lăng trụ: Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song gọi là hai đáy và tất cả các cạnh không thuộc hai cạnh đáy đều song song với nhau.

Trong đó: Các mặt khác với hai đáy gọi là các mặt bên của hình lăng trụ. Cạnh chung của hai mặt bên gọi là cạnh bên của hình lăng trụ. Tùy theo đa giác đáy, ta có hình lăng trụ tam giác, lăng trụ tứ giác … Từ định nghĩa của hình lăng trụ, ta lần lượt suy ra các tính chất sau: a. Các cạnh bên song song và bằng nhau. b. Các mặt bên và các mặt chéo là những hình bình hành. c. Hai đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Định nghĩa hình hộp: Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.

a. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật.

b. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương.

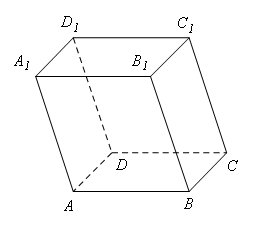Chú ý: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.

5. Hình chóp cụt

Định nghĩa: Cho hình chóp  Một mặt phẳng  song song với mặt phẳng chứa đa giác đáy cắt các cạnh  theo thứ tự tại  Hình tạo bởi thiết diện  và đáy  của hình chóp cùng với các mặt bên  gọi là một hình chóp cụt. Trong đó: Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.

• Các mặt còn lại gọi là các mặt bên của hình chóp cụt.
• Cạnh chung của hai mặt bên kề nhau như gọi là cạnh bên của hình chóp cụt.

Tùy theo đáy là tam giác, tứ giác, ngũ giác,… ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chụp cụt ngũ giác,…

Tính chất: Với hình chóp cụt, ta có các tính chất sau:

1. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.

2. Các mặt bên của hình chóp cụt là các hình thang.

3. Các cạnh bên của hình chóp cụt đồng quy tại một điểm.