SỐ GẦN ĐÚNG, SAI SỐ

Vietlearn
15 minutes

I. LÝ THUYẾT

1. Số gần đúng.

Trong nhiều trường hợp ta không thể biết được giá trị đúng của đại lượng mà ta chỉ biết số gần đúng của nó.

Ví dụ: giá trị gần đúng của IMG_256 là 3,14 hay 3,14159; còn đối với IMG_258 là 1,41 hay 1,414;.Như vậy có sự sai lệch giữa giá trị chính xác của một đại lượng và giá trị gần đúng của nó. Để đánh giá mức độ sai lệch đó, người ta đưa ra khái niệm sai số tuyệt đối.

2. Sai số tuyệt đối:

a) Sai số tuyệt đối của số gần đúng

Nếu a là số gần đúng của IMG_260 thì IMG_262 = IMG_263 được gọi là sai số tuyệt đối của số gần đúng a.

Độ chính xác của một số gần đúng

Trong thực tế, nhiều khi ta không biết IMG_264 nên ta không tính được IMG_266 . Tuy nhiên ta có thể đánh giá IMG_267 không vượt quá một số dương d nào đó.

Nếu IMG_268 thì IMG_269 , khi đó ta viết IMG_271

d gọi là độ chính xác của số gần đúng.

b) Sai số tương đối

Sai số tương đối của số gần đúng a, kí hiệu là δa là tỉ số giữa sai số tuyệt đối và IMG_272 , tức là δa = IMG_274 .

Nhận xét: Nếu IMG_276 thì IMG_277 ≤ d suy ra IMG_278. Do đó IMG_280 càng nhỏ thì chất lượng của phép đo đặc hay tính toán càng cao.

3. Quy tròn số gần đúng

Nguyên tắc quy tròn các số như sau:

Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay chữ số đó và các chữ số bên phải nó bởi 0.

Nếu chữ số ngay sau hàng quy tròn lớn hơn hay bằng 5 thì ta thay chữ số đó và các chữ số bên phải nó bởi 0 và cộng thêm một đơn vị vào số hàng làm tròn.

Nhận xét: Khi thay số đúng bởi số qui tròn đến một hàng số nào đó thì sai số tuyệt đối của số qui tròn không vượt quá nửa đơn vị của hàng qui tròn.

Như vậy, độ chính xác của số qui tròn bằng nửa đơn vị của hàng qui tròn.

Chú ý: Các viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước.

Cho số gần đúng a với độ chính xác d. Khi được yêu cầu quy tròn a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn a đến hàng cao nhất mà d nhỏ hơn một đơn vị của hàng đó.

4. Chữ số chắc (đáng tin)

Cho số gần đúng a của số IMG_281 với độ chính xác d. Trong số a một chữ số được gọi là chữ số chắc (hay đáng tin) nếu d không vượt quá nửa đơn vị của hàng có chữ số đó.

Nhận xét: Tất cả cá chữ số đứng bên trái chữ số chắc đều là chữ số chắc. Tất cả các chữ số đứng bên phải chữ số không chắc đều là chữ số không chắc.

5. Dạng chuẩn của số gần đúng

Nếu số gần đúng là số thập phân không nguyên thì dạng chuẩn là dạng mà mọi chữ số của nó đều là chữ chắc chắn.

Nếu số gần đúng là số nguyên thì dạng chuẩn của nó là: A10k trong đó A là số nguyên, k là hàng thấp nhất có chữ số chắc IMG_282 . (suy ra mọi chữ số của A đều là chữ số chắc chắn).

Khi đó độ chính xác IMG_283 .

6. Kí hiệu khoa học của một số

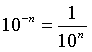Mọi số thập phân khác 0 đều viết được dưới dạng IMG_284 , IMG_285 1≤ IMG_286 <10, IMG_287 (Quy ước IMG_288 ) dạng như vậy được gọi là kí hiệu khoa học của số đó.

II. DẠNG TOÁN

1. Dạng 1: Tính sai số tuyệt đối, độ chính xác của một số gần đúng.

A. VÍ DỤ MINH HỌA

  1. Kết quả đo chiều dài của một cây cầu được ghi là IMG_289 , điều đó có nghĩa là gì?

A. Chiều dài đúng của cây cầu là một số nằm trong khoảng từ IMG_290 đến IMG_291 .

B. Chiều dài đúng của cây cầu là một số lớn hơn 152 m.

C. Chiều dài đúng của cây cầu là một số nhỏ hơn 152 m.

D. Chiều dài đúng của cây cầu là 151,8 m hoặc là 152,2 m.

Giải

Kết quả đo chiều dài của một cây cầu được ghi là IMG_292 có nghĩa là chiều dài đúng của cây cầu là một số nằm trong khoảng từ IMG_293 đến IMG_294 .

  1. Khi tính diện tích hình tròn bán kính R = 3cm, nếu lấy IMG_295 thì độ chính xác là bao nhiêu?

A. IMG_296 . B. IMG_297 . C. IMG_298 . D. IMG_299

Giải

Ta có diện tích hình tròn S = 3,14. 32 và IMG_300 . 32 = IMG_301

Ta có: IMG_302

Do đó: IMG_303

Vậy nếu ta lấy IMG_304 thì diện tích hình tròn là S = 28,26cm2 với độ chính xác IMG_305 .

  1. Cho giá trị gần đúng của 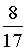IMG_306 là 0,47. Sai số tuyệt đối của 0,47 là:

A. 0,001. B. 0,002. C. 0,003. D. 0,004

Giải

Ta có IMG_307 suy ra sai số tuyệt đối của 0,47 là 0,001.

B. BÀI TẬP TỰ LUYỆN.

  1. Cho giá trị gần đúng của IMG_308 là 0,429. Sai số tuyệt đối của 0,429 là:

A. 0,0001. B. 0,0002. C. 0,0004. D. 0,0005.

  1. Nếu lấy 3,14 làm giá trị gần đúng của p thì sai số là:

A. 0,001. B. 0,002. C. 0,003. D. 0,004.

  1. Cho giá trị gần đúng của IMG_309 là 3,28. Sai số tuyệt đối của số 3,28 là:

A. 0,04. B. 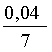IMG_310 . C. 0,06. D. Đáp án khác.

  1. Trái đất quay một vòng quanh mặt trời là 365 ngày. Kết quả này có độ chính xác là IMG_311 ngày. Sai số tuyệt đối là:

A. IMG_312 . B. IMG_313 . C. IMG_314 . D. Đáp án khác.

  1. Người ta đóng bao một vật liệu xây dựng bằng máy, trọng lượng mỗi bao là T = 50 IMG_315 1 (kg). Trong số

các bao được kiểm tra sau đây bao nào không đạt tiêu chuẩn về trọng lượng?

A. 49kg. B. 48,5kg. C. 49,5kg. D. 51kg.

  1. Một hình chữ nhật cố các cạnh: x = 4,2m ± 1cm, y = 7m ± 2cm. Chu vi của hình chữ nhật và sai số tuyệt đối của giá trị đó.

A. 22,4m và 3cm. B. 22,4m và 1cm. C. 22,4m và 2cm. D. 22,4m và 6cm.

  1. Một hình hộp chữ nhật có kích thước x = 3m ± 1cm, y = 5m ± 2cm, z = 4m ± 2cm. Sai số tuyệt đối của thể tích là:

A. 0,72cm3. B. 0,73cm3. C. 0,74cm3. D. 0,75cm3.

Bức thư thứ 28: THỦ DÂM CÓ PHẢI LÀ CHUYỆN RẤT XẤU KHÔNG?
  1. Hình chữ nhật có các cạnh: x = 2m ± 1cm, y = 5m ± 2cm. Diện tích hình chữ nhật và sai số tuyệt đối của giá trị đó là:

A. 10m2 và 900cm2. B. 10m2 và 500cm2. C. 10m2 và 400cm2. D. 10m2 và 1404cm2.

  1. Cho số IMG_316 . Cho các giá trị gần đúng của x là 0,28; 0,29; 0,286; 0,287. Giá trị gần đúng nào là tốt nhất

A. 0,28. B. 0,29. C. 0.286. D. 0,3.

  1. Một hình hộp chữ nhật có kích thước x = 3m ± 1cm, y = 5m ± 2cm, z = 4m ± 2cm. Sai số tuyệt đối của thể tích là:

A. 0,72cm3. B. 0,73cm3. C. 0,74cm3. D. 0,75cm3.

  1. Cho tam giác ABC có độ dài ba cạnh IMG_317 ; IMG_318 ; IMG_319 . Tính chu vi P của tam giác đó.

A. IMG_320 . B. IMG_321 .

C. IMG_322 . D. IMG_323

2. Dạng 2: Sai số tương đối của số gần đúng

A. VÍ DỤ MINH HỌA

  1. Kết quả đo chiều dài của một cây cầu được ghi là 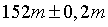IMG_324 . Tìm sai số tương đối của phép đo chiều dài cây cầu.

A. IMG_325 . B. IMG_326 . C. IMG_327 . D. IMG_328

Giải

  1. Bạn A đo chiều dài của một sân bóng ghi được 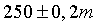IMG_329 . Bạn B đo chiều cao của một cột cờ được 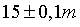IMG_330 . Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?

A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.

B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.

C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.

D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%.

Giải

Phép đo của bạn A có sai số tương đối 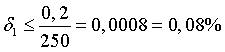IMG_331

Phép đo của bạn B có sai số tương đối 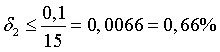IMG_332

Như vậy phép đo của bạn A có độ chính xác cao hơn.

  1. Hãy xác định sai số tuyệt đối của số 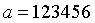IMG_333 biết sai số tương đối IMG_334

A. 146,912. B. 617280. C. 24691,2. D. 61728000

Giải

Ta có IMG_335 .

B. BÀI TẬP TỰ LUYỆN.

  1. Độ dài của cầu Bến Thủy 2 (Nghệ An) người ta đo được là IMG_336 . Sai số tương đối tối đa trong phép đo đó là bao nhiêu?

A. IMG_337 . B. IMG_338 . C. IMG_339 . D. IMG_340 .

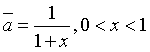  1. Cho IMG_341 . Giả sử ta lấy số IMG_342 làm giá trị gần đúng của IMG_343 . Hãy tính sai số tương đối của a theo x.

A. IMG_344 . B. IMG_345 . C. IMG_346 . D. IMG_347 .

  1. Một vật thể có thể tích là IMG_348 . Sai số tương đối của giá trị gần đúng ấy là:

A. 0,01%. B. 0,03%. C. 0,04%. D. 0,05%.

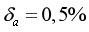
  1. Hãy xác định sai số tuyệt đối của số IMG_349 biết sai số tương đối IMG_350

A. 0,0062179. B. 0,00062179. C. 0,062179. D. 0,00248716.

  1. Hình chữ nhật có các cạnh: x = 2m ± 1cm, y = 5m ± 2cm. Diện tích hình chữ nhật và sai số tương đối của giá trị đó là:

A. 10m2 và 50/00. B. 10m2 và 40/00. C. 10m2 và 90/00. D. 10m2 và 200/00.

  1. Hình chữ nhật có các cạnh: x = 2m ± 1cm, y = 5m ± 2cm. Chu vi hình chữ nhật và sai số tương đối của giá trị đó là :

A. 22,4m và 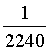IMG_351 . B. 22,4m và 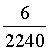IMG_352 . C. 22,4m và 6cm. D. Một đáp số khác

3. Dạng 3 : Quy tròn số gần đúng

Phương pháp giải

Tùy theo mức độ cho phép, ta có thể quy tròn một số đếm đến hàng đơn vị, hang chục, hang trăm,… hay đến hàng phần chục, hàng phần trăm,… (gọi là hàng quy tròn) theo nguyên tắc sau:

Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0.

Nếu chữ số ngay sau hàng quy tròn lớn hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0 và cộng thêm một đơn vị ở chữ số ở hàng quy tròn.

Ví dụ: Các số quy tròn của số x theo từng hàng cho trong bảng sau:

Quy tròn đến Hàng chục Hàng đơn vị Hàng phần chục Hàng phần trăm Hàng phần nghìn
x = 549,2705 550 549 549,3 549,27 549,271
x = 397,4619 400 397 397,5 397,46 397,462

Nhận xét:

Khi thay số đúng bởi số quy tròn thì sai số tuyệt đối không vượt quá nửa đơn vị của hàng quy tròn.

Nếu IMG_353 thì ta quy tròn số IMG_354 đến hàng lớn hơn hàng của IMG_355 một đơn vị.

A. VÍ DỤ MINH HỌA

  1. Tìm số gần đúng của a = 2851275 với độ chính xác d = 300

A. 2851000. B. 2851575. C. 2850025. D. 2851200

Giải

Vì độ chính xác đến hàng trăm nên ta quy tròn a đến hàng nghìn, vậy số quy tròn của a là 2851000.

  1. Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001.

A. 5,25. B. 5,24. C. 5,246. D. 5,2

Giải

Vì độ chính xác đến hàng phần nghìn nên ta quy tròn a đến hàng phần trăm, vậy số quy tròn của a là 5,25.

  1. Sử dụng mãy tính bỏ túi, hãy viết giá trị gần đúng của IMG_356 chính xác đến hàng phần trăm

A. 1,73. B. 1,732. C. 1,7. D. 1,7320

Giải

Sử dụng máy tính bỏ túi ta có IMG_357 = 1,732050808. Do đó: Giá trị gần đúng của IMG_358 chính xác đến hàng phần trăm là 1,73.

  1. Sử dụng mãy tính bỏ túi, hãy viết giá trị gần đúng của IMG_359 chính xác đến hàng phần nghìn.

A. 9,870. B. 9,869. C. 9,871. D. 9,8696

Giải

Sử dụng máy tính bỏ túi ta có giá trị của IMG_360 là 9,8696044. Do đó giá trị gần đúng của IMG_361 chính xác đến hàng phần nghìn là 9,870.

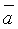
  1. Hãy viết số quy tròn của số a với độ chính xác d được cho sau đây: IMG_362 IMG_363 = 17658 ± 16.

A. 17700. B. 17660. C. 18000. D. 17674

Giải

Vì độ chính xác đến hàng chục nên ta phải quy tròn số 17638 đến hàng trăm. Vậy số quy tròn là 17700 (hay viết IMG_364 ≈ 17700).

B. BÀI TẬP TỰ LUYỆN.

  1. Cho số gần đúng IMG_365 với độ chính xác IMG_366 . Hãy viết số quy tròn của số a

A. 23749000. B. 23748000. C. 23746000. D. 23747000.

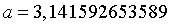  1. Cho giá trị gần đúng của IMG_367 là IMG_368 với độ chính xác IMG_369 . Hãy viết số quy tròn của số a

A. IMG_370 . B. IMG_371 . C. IMG_372 . D. IMG_373 .

  1. Hãy viết số quy tròn của số gần đúng 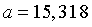IMG_374 biết IMG_375

A. 15,3. B. 15,31. C. 15,32. D. 15,4.

  1. Đo độ cao một ngọn cây là IMG_376 Hãy viết số quy tròn của số gần đúng 347,13

A. 345. B. 347. C. 348. D. 346

Máy bay đều muốn bay cao phải không?