THỐNG KÊ

I – LÝ THUYẾT

I.1 – BẢNG PHÂN BỐ TẦN SỐ VÀ TẦN SUẤT

I.1.1 – Một số khái niệm cơ bản:

· Một tập con hữu hạn các đơn vị điều tra được gọi là một mẫu.

· Số phần tử của một mẫu được gọi là kích thước mẫu.

· Các giá trị của dấu hiệu thu được trên mẫu được gọi là một mẫu số liệu.

Chú ý: Khi thực hiện điều tra thống kê (theo mục đích định trước), cần xác định tập hợp các đơn vị điều tra, dấu hiệu điều tra và thu thập các số liệu.

Ví dụ: Số liệu thông kê điểm kiểm tra môn toán của lớp 10A

7 7 6  6 8   6 5 5   9 10 9 10 9 5 4  6 7 5 8 6  7  5 8 7 6    6 9 4   6 8 9 9  5 6 7 7  6 8  4 9 7 7 8 6 5

I.1.2 – Định nghĩa:

Giả sử dãy số liệu thống kê đã cho có giá trị khác nhau . Gọi là một giá trị bất kì trong giá trị đó, ta có:

Tần số: số lần xuất hiện giá trị x_i trong dãy số liệu đã cho gọi là tần số của giá trị đó, kí hiệu là .

Ví dụ: Trong bảng số liệu trên ta thấy có 7 giá trị khác nhau là

xuất hiện 3 lần (tần số của là 3) Tần suất: Số được gọi là tần suất của giá trị (tỉ lệ của , tỉ lệ phần trăm)

Ví dụ: x₁ có tần số là 3, do đó: hay = 5%

I.1.3 – Bảng phân bố tần suất và tần số

Tên dữ liệu	Tần số	Tần suất (%)
x1 x2 . . xk	n1 n2 . . nk	f1 f2 . . fk
Cộng	n1+…+nk	100 %

Ví dụ: Bảng phân bố tần số và tần suất điểm kiểm tra 15’ môn toán 10CB

Điểm toán	Tần số	Tần suất ( %)
4 5 6 7 8 9 10	3 7 11 9 6 7 2	6,67 15,56 24,44 20 13,33 15,6 4,4
Cộng	45	100%

Chú ý: Nếu bỏ cột tầng số thì ta được bảng phân bố tần suất; bỏ cột tần suất thì ta được bảng phân bố tần số.

I.1.4 – Bảng phân bố tần số và tần suất ghép lớp

Giả sử dãy số liệu thông kê đã cho được phân vào lớp ( ). Xét lớp thứ trong lớp đó, ta có:

Số các số liệu thông kê thuộc lớp thứ được tần số của lớp đó.

Số được gọi là tần số của lớp thứ

Ví dụ: Theo bảng thông kê trên ta có thể phân thành 3 lớp [4;7), [7;9), [9;10]

Lớp điểm  toán	Tần số	Tần suất ( %)
[4;7) [7;9) [9;10]	21 15 9	46,67 33,33 20
Cộng	45	100%

Bảng này gọi là bảng phân bố tần số và tần suất ghép lớp. Nếu bỏ cột tần số thì ta được bảng phân bố tần suất ghép lớp; Nếu bỏ cột tần suất thì ta được bảng phân bố tần số ghép lớp.

I.1.5 – BÀI TẬP MẪU

Dạng 1: lập bảng phân bố tần số và tần suất

Phương pháp: để lập bảng phân bố tần số – tần suất từ số liệu ban đầu, ta thực hiện các bước:

• Sắp thứ tự mẫu số liệu
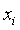• Tính tần số của các giá trị bằng cách đếm số lần 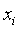xuất hiện
• Tính tần suất của theo công thức với 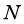là kích thước của mẫu
• Đặt các số liệu , , 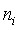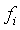vào bảng

Bài tập 1: Chiều cao của một nhóm học sinh gồm 30 em (đv: m ) của lớp 10 được liệt kê ở bảng sau:

1.45	1.58	1.51	1.52	1.52	1.67
1.50	1.60	1.65	1.55	1.55	1.64
1.47	1.70	1.73	1.59	1.62	1.56
1.48	1.48	1.58	1.55	1.49	1.52
1.52	1.50	1.60	1.50	1.63	1.71

Hãy lập bảng phân bố tần số – tần suất.

Giải

Ta có bảng phân bố tần số – tần suất:

Chiều cao	Tần số	Tần suất
1.45	1	3.33
1.47	1	3.33
1.48	2	6.67
1.49	1	3.33
1.50	3	10.0
1.52	4	13.33
1.55	3	10.0
1.56	1	3.33
1.58	2	6.67
1.59	1	3.33
1.60	2	6.67
1.61	1	3.33
1.62	1	3.33
1.63	1	3.33
1.64	1	3.33
1.65	1	3.33
1.67	1	3.33
1.70	1	3.33
1.71	1	3.33
1.73	1	3.33
Cộng		100%

Bài tập 2:Số lượng khách đến tham quan một điểm du lịch trong 12 tháng được thống kê như ở bảng sau:

Tháng	1	2	3	4	5	6	7	8	9	10	11	12
Số khách	430	550	430	520	550	515	550	110	520	430	550	880

Lập bảng phân bố tần số – tần suất

Giải

Ta có bảng phân bố tần số – tần suất

Số lượng khách ( người )	Tần số	Tần suất%
110	1	8,3
430	3	24,9
515	1	8,3
520	2	16,8
550	4	33,4
800	1	8,3
Cộng	N= 12	100%

Dạng 2: lập bảng phân bố tần số – tần suất ghép lớp

Bài tập 1: Chiều cao của một nhóm học sinh gồm 30 em (đv: m ) của lớp 10 được liệt kê ở bảng sau:

1.45	1.58	1.51	1.52	1.52	1.67
1.50	1.60	1.65	1.55	1.55	1.64
1.47	1.70	1.73	1.59	1.62	1.56
1.48	1.48	1.58	1.55	1.49	1.52
1.52	1.50	1.60	1.50	1.63	1.71

Hãy lập bảng phân bố tần số – tần suất ghép lớp với các lớp là: ; ;

Giải

Tần số của lớp 1: là ; tần suất

Tần số của lớp 2: là ; tần suất

Tần số của lớp 3: là ; tần suất

Bảng phân bố tần số – tần suất ghép lớp

Lơp chiều cao (m)	Tần số	Tần suất (%)
	12	40.00
	13	43.33
	5	16.67
Cộng	N=30	100%

Bài tập 2: Cho các số liệu thống kê ghi trong bảng sau :

Thành tích chạy 500m của học sinh lớp 10A ở trường THPT C. ( đơn vị : giây )

6,3	6,2	6,5	6,8	6,9	8,2	8,6	6,6	6,7	7,0	7,1
8,5	7,4	7,3	7,2	7,1	7,0	8,4	8,1	7,1	7,3	7,5
8,7	7,6	7,7	7,8	7,5	7,7	7,8	7,2	7,5	8,3	7,6

Lập bảng phân bố tần số – tần suất ghép lớp với các lớp :

[ 6,0 ; 6,5 ) ; [ 6,5 ; 7,0 ) ; [ 7,0 ; 7,5 ) ; [ 7,5 ; 8,0 ) ; [ 8,0 ; 8,5 ) ; [ 8,5 ; 9,0 ]

Giải

Tần số của lớp 1: [ 6,0 ; 6,5 ) là ; tần suất

Tấn số của lớp 2: [ 6,5 ; 7,0 ) là ; tần suất

Tần số của lớp 3: [ 7,0 ; 7,5 ) là ; tần suất

Tần số của lớp 4: [ 7,5 ; 8,0 ) là ; tần suất

Tần số của lớp 5: [ 8,0 ; 8,5 ) là ; tần suất

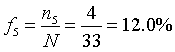
Tần số của lớp 6: [ 8,5 ; 9,0 ] là ; tần suất

Bảng phân bố tần số – tần suất ghéo lớp là

Lớp Thành Tích ( m )	Tần số	Tần suất %
[6,0; 6,5)	2	6,0
[6,5; 7,0)	5	15,2
[7,0; 7,5)	10	30,4
[7,5; 8,0)	9	27,4
[8,0; 8,5)	4	12,0
[8,5; 9,0]	3	9,0
	N= 33	100%

I.2 – BIỂU ĐỒ

I.2.1 – Biểu đồ tần suất hình cột:

Cách vẽ:

• Vẽ hai đường thẳng vuông góc. Trên đường thẳng nằm ngang (dùng làm trục số) ta đánh dáu các khoảng xác định lớp.
• Tại mỗi khoảng ta dựng lên một hình cột chữ nhật, với đáy là khoảng đó, còn chiều cao bằng tần suất của lớp mà khoảng đó xác định

I.2.2 – Đường gấp khúc tần suất

Cách vẽ: Ta vẽ hai đường thẳng vuông góc ( như hình vễ biểu đồ hình cột). Trên mặt phẳng tọa độ xác định các điểm sau đó vẽ các đoạn thẳng nối các điểm với các điểm ta thu được một đường gấp khúc. Đường gấp khúc này gọi là đường gấp khúc tần suất.

I.2.3 – Biểu đồ hình quạt:

Cách vẽ: vẽ hình tròn, chia hình tròn thành những hình quạt, mỗi lớp tương ứng với một hình quạt mà diện tích của nó tỉ lệ với tần suất của lớp đó.