TỌA ĐỘ CỦA ĐIỂM VÀ VÉCTƠ TRONG KHÔNG GIAN

A – LÝ THUYẾT CHUNG

1. Véc tơ trong không gian

* Định nghĩa

Trong không gian, vecto là một đoạn thẳng có định hướng tức là đoạn thẳng có quy định thứ tự của hai đầu

ü Chú ý: Các định nghĩa về hai vecto bằng nhau, đối nhau và các phép toán trên các vecto trong không gian được xác định tương tự như trong mặt phẳng.

2. Vecto đồng phẳng

* Định nghĩa: Ba vecto khác gọi là đồng phẳng khi giá của chúng cùng song song với một mặt phẳng.

Chú ý:

· vecto khác gọi là đồng phẳng khi giá　của chúng cùng song song với một mặt phẳng.

· Các giá của các vecto đồng phẳng có thể là các đường thẳng chéo nhau.

* Điều kiện để 3 vecto khác đồng phẳng

Định lý 1:

đồng phẳng :

* Phân tích một vecto theo ba vecto không đồng phẳng

· Định lý 2: Cho 3 vecto không đồng phẳng. Bất kì một vecto nào trong không gian cũng có thể phân tích theo ba vecto đó, nghĩa la có một bộ ba số thực duy nhất

ü Chú ý: Cho vecto khác :

1. đồng phẳng nếu có ba số thực không đồng thời bằng 0 sao cho:

2. không đồng phẳng nếu từ

3. Tọa độ của vecto

Trong không gian xét hệ trục có trục vuông góc với trục tại O, và trục vuông góc với mặt phẳng tại O. Các vecto đơn vị trên từng trục lần lượt là

a)

b)

c) Cho ta có:

và

d) M là trung điểm thì

e) Cho và ta có:

·

·

·

·

·

· (với )

· và vuông góc:

· và cùng phương:

4. Tích có hướng và ứng dụng

Tích có hướng của và là:

a. Tính chất:

·

·

· và cùng phương:

· đồng phẳng

b. Các ứng dụng tích có hướng

· Diện tích tam giác:

· Thể tích tứ diện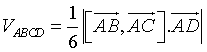

· Thể tích khối hộp:

5. Một số kiến thức khác

a) Nếu  chia đoạn AB theo tỉ số  thì ta có:  với b) G là trọng tâm tam giác c) G là trọng tâm tứ diện

B – CÁC DẠNG TOÁN CƠ BẢN

Dạng 1. thẳng hàng cùng phương .

Dạng 2. là ba đỉnh tam giác không thẳng hàng không cùng phương .

Dạng 3. là trọng tâm tam giác thì:

Dạng 4. Cho có các chân của các đường phân giác trong và ngoài của góc của trên . Ta có: ,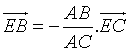

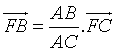
Dạng 5. diện tích của hình bình hành là:

Dạng 6. Đường cao của :

Dạng 7. Tìm sao cho là hình bình hành: Từ t/c hbh có 4 cặp vecto bằng nhau hoặc tọa độ .

Dạng 8. Chứng minh là một tứ diện không đồng phẳng .

Dạng 9. là trọng tâm tứ diện thì:

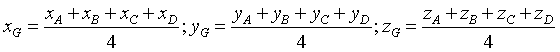
Dạng 10. Thể tích khối tứ diện :

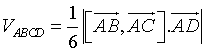
Dạng 11. Đường cao của tứ diện :

Dạng 12. Thể tích hình hộp: .

Dạng 13. Hình chiếu của điểm lên các mặt phẳng tọa độ và các trục:
Xem lại mục 1, công thức 17, 18.

Dạng 14. Tìm điểm đối xứng với điểm qua các mặt phẳng tọa độ, các trục và gốc tọa độ:
(Thiếu tọa độ nào thì đổi dấu tọa độ đó, có mặt tọa độ nào thì để nguyên tọa độ đó)

: : :

: : :
Qua gốc :

C – BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho 4 điểm là:

A. Tứ diện. B. Hình chóp đều.

C. Tứ diện đều. D. Hình thang vuông

Câu 2: Cho bốn điểm Gọi lần lượt là trung điểm của và Khi đó là:

A. Hình chóp. B. Hình chóp đều. C. Tứ diện đều. D. Tam diện vuông

Câu 3: Cho bốn điểm Xác định tọa độ trọng tâm G của hình chóp

A. . B. . C. . D.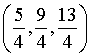

Câu 4: Cho 3 vectơ Xác định vec tơ thỏa mãn

A. . B. . C. . D. .

Câu 5: Trong không gian Oxyz, cho điểm . Điểm D trong mặt phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là:

A. B. C. D.

Câu 6: Trong không gian với hệ tọa độ , cho ba điểm , , . Tìm tọa độ điểm sao cho là hình thang có hai cạnh đáy , và có góc bằng

A. . B. . C. . D. .

Câu 7: Trong không gian với hệ tọa độ , cho hình hộp chữ nhật có trùng với gốc tọa độ , các đỉnh , , với và . Gọi là trung điểm của cạnh . Khi đó thể tích tứ diện đạt giá trị lớn nhất bằng

A. . B. . C. . D. .

Câu 8: Cho ba điểm . Nếu tam giác thỏa mãn hệ thức thì có tọa độ trọng tâm là:

A. B. C. D.

Câu 9: Trong không gian với hệ trục tọa độ , cho ba điểm . Biết , thể tích tứ diện bằng 3. Giá trị của biểu thức bằng

A. B. C. D.

Câu 10: Cho hình chóp biết . Gọi là trung điểm của . Để khối chóp có thể tích bằng (đvtt) thì có hai điểm thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm của

A. . B. C. . D.