Ứng dụng đơn điệu trong giải phương trình, hệ phương trình, bất phương trình và hệ bất phương trình
Trong khuôn khổ chương trình, tác giả chỉ đề cập những bài tập thường gặp. Bạn đọc muốn nghiên cứu kĩ về ứng dụng đơn điệu trong việc giải phương trình…, vui lòng tìm đọc tập sách: Đại số – lượng giác.
Phương pháp .
Biến đổi phương trình ,bất phương trình đã cho thành dạng f(x) = g(m) ,
f(x) > g(m),…Sau đó lập bảng biến thiên của f(x) , dựa vào bảng biến thiên này sẽ tìm được các giá trị của tham số thỏa yêu cầu của bài toán.
Dựa vào định nghĩa hàm số đồng biến, hàm số nghịch biến ta thấy
![]() Nếu hàm số
Nếu hàm số ![]() liên tục và đồng biến trên D thì :
liên tục và đồng biến trên D thì :
![]() và
và ![]() .
.
![]() Nếu hàm số
Nếu hàm số ![]() liên tục và nghịch biến trên D thì :
liên tục và nghịch biến trên D thì :
![]() và
và ![]() .
.
Từ đó gợi cho chúng ta ứng dụng vào các bài toán chứng minh bất đẳng thức và các bài toán giải phương trình, bất phương trình. Cụ thể ta có các tính chất sau:
Tính chất 1: Nếu hàm số ![]() liên tục và luôn đồng biến (hoặc luôn nghịch biến) trên
liên tục và luôn đồng biến (hoặc luôn nghịch biến) trên ![]() thì số nghiệm của phương trình :
thì số nghiệm của phương trình : ![]() (trên
(trên ![]() ) không nhiều hơn một và
) không nhiều hơn một và ![]()
![]() .
.
Chứng minh: Ta giả sử ![]() là hàm đồng biến trên
là hàm đồng biến trên ![]()
![]() Nếu
Nếu ![]()
![]() Nếu
Nếu ![]()
Tính chất 2: Nếu hàm số ![]() liên tục và luôn đồng biến (hoặc luôn nghịch biến) ; hàm số
liên tục và luôn đồng biến (hoặc luôn nghịch biến) ; hàm số ![]() liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình :
liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình : ![]() không nhiều hơn một.
không nhiều hơn một.
Chứng minh: Giả sử ![]() đồng biến còn
đồng biến còn ![]() nghịch biến trên
nghịch biến trên ![]() và
và ![]() .
.
* Nếu ![]() vô nghiệm
vô nghiệm
* Nếu ![]() vô nghiệm
vô nghiệm
Vậy ![]() là nghiệm duy nhất của phương trình
là nghiệm duy nhất của phương trình ![]() .
.
Tính chất 3: Nếu hàm số ![]() liên tục và luôn đồng biến ( hoặc luôn nghịch biến) trên
liên tục và luôn đồng biến ( hoặc luôn nghịch biến) trên ![]() thì
thì ![]() .
.
Tính chất 4: Cho hàm số ![]() liên tục trên [a;b] và có đạo hàm trên khoảng liên tục
liên tục trên [a;b] và có đạo hàm trên khoảng liên tục ![]() . Nếu
. Nếu ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm thuộc khoảng
có ít nhất một nghiệm thuộc khoảng ![]() .
.
Chứng minh:
Giả sử phương trình ![]() vô nghiệm trên
vô nghiệm trên ![]() .
.
Khi đó ![]() (hoặc
(hoặc ![]() ).
).
Suy ra ![]() (hoặc
(hoặc ![]() ).
).
Điều này trái với giả thiết ![]() .
.
Vậy phương trình ![]() có ít nhất một nghiệm trên
có ít nhất một nghiệm trên ![]() .
.
Từ định lí này, ta có được hai hệ quả sau:
Hệ quả 1: Nếu phương trình ![]() có m nghiệm thì phương trình
có m nghiệm thì phương trình ![]() có
có ![]() nghiệm.
nghiệm.
Hệ quả 2: Cho hàm số ![]() có đạo hàm đến cấp k liên tục trên
có đạo hàm đến cấp k liên tục trên ![]() . Nếu phương trình
. Nếu phương trình ![]() có đúng m nghiệm thì phương trình
có đúng m nghiệm thì phương trình ![]() có nhiều nhất là
có nhiều nhất là ![]() nghiệm.
nghiệm.
Thật vậy: Giả sử phương trình ![]() có nhiều hơn m+1 nghiệm thì phương trình
có nhiều hơn m+1 nghiệm thì phương trình ![]() có nhiều hơn m nghiệm, điều này trái với giả thiết bài toán.
có nhiều hơn m nghiệm, điều này trái với giả thiết bài toán.
Từ hệ quả 2 ![]() nếu
nếu ![]() có một nghiệm thì
có một nghiệm thì ![]() có nhiều nhất hai nghiệm.
có nhiều nhất hai nghiệm.
Chú ý: Sử dụng tính đơn điệu để giải phương trình – bất phương trình ta thường đi theo hai hướng sau:
Hướng 1: Đưa phương trình về dạng ![]() , trong đó
, trong đó ![]() là một hàm số liên tục và luôn đồng biến hoặc luôn nghịch biến trên tập đang xét.
là một hàm số liên tục và luôn đồng biến hoặc luôn nghịch biến trên tập đang xét.
Để làm theo hướng này, chúng ta cần nhẩm trước một nghiệm của phương trình và nhận diện được tính đơn điệu của hàm số f.
![]() Để nhẩm nghiệm, ta có thể sử dụng máy tính bỏ túi để tìm nghiệm.
Để nhẩm nghiệm, ta có thể sử dụng máy tính bỏ túi để tìm nghiệm.
Cụ thể: Để tìm một nghiệm của phương trình ![]() ta thực hiện như sau
ta thực hiện như sau
Bước 1: Nhập biểu thức ![]() (Dùng phím ALPHA+ X)
(Dùng phím ALPHA+ X)
Bước 2: Dùng lệnh giải phương trình: SHIFT+CALC (SOLVE) nhập giá trị của X (nhập giá trị bất kì) =.
![]() Để nhận diện được tính đơn điệu của hàm số f, chúng ta cần chú ý
Để nhận diện được tính đơn điệu của hàm số f, chúng ta cần chú ý
*Tổng hai hàm số đồng biến là một hàm số đồng biến
* Hàm số đối của một hàm số đồng biến là một hàm số nghịch biến.
* Nếu hàm số ![]() đồng biến thì
đồng biến thì ![]() là hàm số đồng biến.
là hàm số đồng biến.
* Nếu hàm số ![]() đồng biến và nhận giá trị dương thì hàm số
đồng biến và nhận giá trị dương thì hàm số 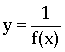 là một hàm nghịch biến.
là một hàm nghịch biến.
Hướng 2: Biến đổi phương trình về dạng: ![]() , trong đó
, trong đó ![]() là các hàm theo x.
là các hàm theo x.
Làm theo hướng ta thường áp dụng khi gặp phương trình chứa hai phép toán ngược nhau.
Chú ý 1:
Ký hiệu ![]() là một đoạn,một khoảng hoặc một nửa khoảng.
là một đoạn,một khoảng hoặc một nửa khoảng.
![]() Nếu
Nếu ![]() liên tục trên đoạn
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm
có ít nhất một nghiệm ![]() .
.
![]() Nếu
Nếu ![]() liên tục và đơn điệu trên
liên tục và đơn điệu trên ![]() thì phương trình
thì phương trình ![]() có không quá một nghiệm trên
có không quá một nghiệm trên ![]() .
.
Chú ý 2:
Nếu ![]() liên tục và tăng trên
liên tục và tăng trên ![]() ,
, ![]() liên tục và giảm (hoặc là hàm hằng) trên
liên tục và giảm (hoặc là hàm hằng) trên ![]() thì phương trình
thì phương trình ![]() có không quá một nghiệm trên
có không quá một nghiệm trên ![]() .
.
![]() Nếu phương trình
Nếu phương trình ![]() có
có ![]() nghiệm trên khoảng
nghiệm trên khoảng ![]() thì phương trình
thì phương trình ![]() có không quá
có không quá ![]() nghiệm trên khoảng
nghiệm trên khoảng ![]() .
.
![]() Tổng của
Tổng của ![]() hàm tăng trên
hàm tăng trên ![]() là một hàm tăng trên
là một hàm tăng trên ![]() , tổng của
, tổng của ![]() hàm giảm trên
hàm giảm trên ![]() là một hàm giảm trên
là một hàm giảm trên ![]() .
.
![]() Nếu
Nếu ![]() là hàm tăng trên
là hàm tăng trên ![]() thì
thì ![]() tăng trên
tăng trên ![]() nếu
nếu ![]() và
và ![]() giảm trên
giảm trên ![]() nếu
nếu ![]() .
.
Các ví dụ
Ví dụ 1. Giải phương trình:
1. ![]() Đề thi Cao đẳng năm 2012
Đề thi Cao đẳng năm 2012
2. ![]()
3. ![]() Đề thi Đại học khối B năm 2010
Đề thi Đại học khối B năm 2010
4. ![]()
Lời giải.
1. Điều kiện: ![]() .
.
Phương trình đã cho tương đương với: ![]()
![]()
Xét hàm số: ![]() trên
trên ![]() .
.
Ta có: ![]() , suy ra
, suy ra ![]() đồng biến trên
đồng biến trên ![]()
Do đó ![]()

2. Nhận xét đặc điểm các biểu thức dưới dấu căn ta thấy ở mỗi vế biểu thức dưới dấu căn hơn kém nhau 1. Do đó nếu ta đặt đặt ![]()
![]() thì phương trình đã cho trở thành:
thì phương trình đã cho trở thành: ![]() .
.
Trong đó ![]() , có:
, có:  nên f(t) là hàm đồng biến.
nên f(t) là hàm đồng biến.
Do đó: ![]()
Vậy phương trình có hai nghiệm: ![]() .
.
3. Điều kiện: 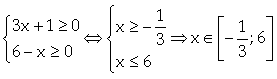
Dễ thấy ![]() hoặc
hoặc ![]() không là nghiệm phương trình.
không là nghiệm phương trình.
Cách 1: Xét hàm số: ![]() liên tục trên khoảng
liên tục trên khoảng  .
.
Ta có: 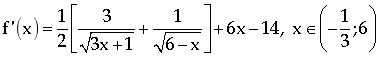
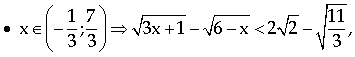
 .
.
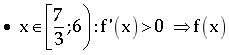 đồng biến trên
đồng biến trên  và
và ![]() .
.
Do đó trên  phương trình
phương trình ![]() có đúng 1 nghiệm
có đúng 1 nghiệm ![]() .
.
Vậy phương trình có nghiệm duy nhất ![]() .
.
Cách 2: Phương trình : ![]()
![]()

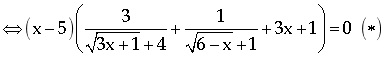
Vì  nên phương trình
nên phương trình
![]() .
.
Vậy phương trình cho có nghiệm duy nhất ![]() .
.
4. Điều kiện: ![]() .
.
Dễ thấy, ![]() hoặc
hoặc ![]() không là nghiệm phương trình.
không là nghiệm phương trình.
Phương trình cho viết lại: ![]()
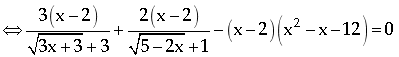

Xét hàm số ![]() , với
, với  .
.
Ta có: ![]() và
và ![]()
 , do đó
, do đó  , mọi
, mọi 
Vậy, phương trình cho có nghiệm duy nhất ![]() .
.
Ví dụ 2 : Giải phương trình: ![]()
Lời giải.
Điều kiện xác định: ![]() .
.
Phương trình đã cho tương đương: ![]()
![]()
![]()
Đặt ![]() với x thuộc
với x thuộc 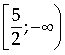
Ta có:  với
với ![]()
![]() hàm số
hàm số ![]() đồng biến trên
đồng biến trên 
![]() phương trình
phương trình ![]() có tối đa một nghiệm
có tối đa một nghiệm
Và ![]() (2). Từ (1) và (2) suy ra phương trình đã cho có nghiệm duy nhất
(2). Từ (1) và (2) suy ra phương trình đã cho có nghiệm duy nhất ![]() .
.