ỨNG DỤNG TÍCH VÔ HƯỚNG CỦA HAI VECTƠ ĐỂ GIẢI MỘT SỐ DẠNG TOÁN
Tích vô hướng của hai vectơ một phần nhỏ trong chương trình Hình học 10. Tuy vậy tích vô hướng của hai vec tơ đóng vai trò quan trọng trong Hình học nói riêng và trong toán học nói chung.
Trong các kì thi ta thường thấy xuất hiện một số bài toán giải phương trình, bất phương trình, hệ phương trình, hay chúng minh một số bất đẳng thức hoăc các bài toán về cực trị. Những bài toán toán đó nếu ta gặp dạng của chúng và biết được các phương pháp giải của từng dạng thì đó là điều khá đơn giản. Tuy vậy có những bài toán có độ khó nhất định đối với học sinh bởi vì sự đa dạng của nó và để giải được thì chúng ta cần kết hợp nhiều kiến thức liên quan đến chúng, trong đó tích vô hướng của hai vectơ ứng dụng quan trọng trong một số dạng Toán như các bài toán giải phương trình, bất phương trình, hệ phương trình, hay chúng minh một số đẳng thức và bất đẳng thức, hoăc các bài toán về cực trị.
Xuất phát từ tầm quan trọng của nội dung và thực trạng trên, để học sinh có thể dễ dàng và tự tin hơn khi gặp một số bài toán giải phương trình, bất phương trình, hệ phương trình, hay chúng minh một số bất đẳng thức hoặc các bài toán về cực trị, giúp các em phát huy được khả năng phân tích, tổng hợp, khái quát hóa qua các bài tập nhỏ, cùng với sự tích lủy kinh nghiệm của bản thân qua những năm giảng dạy, tôi đưa ra bài viết này. Hy vọng đó là tài liệu tham khảo nhỏ của quý thầy cô và các bạn học sinh.
I. ĐỊNH NGHĨA TÍCH VÔ HƯỚNG CỦA HAI VÉCTƠ VÀ ỨNG DỤNG ĐỂ
GIẢI MỘT SỐ DẠNG TOÁN
- Định nghĩa:
Cho hai véctơ ![]() , tích vô hướng của hai véc tơ được định nghĩa như sau:
, tích vô hướng của hai véc tơ được định nghĩa như sau:
![]() (I), với
(I), với ![]() là góc giữa hai véctơ
là góc giữa hai véctơ
Suy ra: 
Biểu thức tọa độ của tích vô hướng:
– Trong hệ tọa độ Descartes vuông góc Oxy cho ![]()
thì ![]()
– Trong hệ tọa độ Descartes vuông góc Oxyz cho ![]()
thì ![]()
2. Ứng dụng tích vô hướng của hai vectơ
Từ công thức (I) ta có thể vận dụng để chứng minh hai đường thẳng hoặc là song song hoặc là vuông góc hoặc tính góc tạo bởi hai đường thẳng. Tuy nhiên, nếu dừng ở đó thì chưa thấy hết được ứng dụng của nó. Chỉ cần chú ý rằng ![]() thì từ (I) ta có thể suy ra các bất đẳng thức:
thì từ (I) ta có thể suy ra các bất đẳng thức:
![]() (II)
(II)
![]() (III)
(III)
- Trong hệ tọa độ Descartes vuông góc Oxy cho
 thì biểu thức giải tích của (II) và (III) là
thì biểu thức giải tích của (II) và (III) là
![]() (II1)
(II1)
![]() (III1)
(III1)
(II) trở thành đẳng thức khi ![]() cùng hướng,còn (III) khi trở thành đẳng thức khi
cùng hướng,còn (III) khi trở thành đẳng thức khi ![]() cùng phương,tức là
cùng phương,tức là ![]() hay
hay
 (IV1)
(IV1)
với ![]() k > 0 khi
k > 0 khi ![]() cùng hướng, k < 0 khi
cùng hướng, k < 0 khi ![]() cùng phương khác hướng.
cùng phương khác hướng.
- Trong hệ tọa độ Descartes vuông góc Oxyz cho
 thì biểu thức giải tích của (II) và (III) là
thì biểu thức giải tích của (II) và (III) là
![]() (II’)
(II’)
![]() (III’)
(III’)
(II) trở thành đẳng thức khi ![]() cùng hướng,còn (III) khi trở thành đẳng thức khi
cùng hướng,còn (III) khi trở thành đẳng thức khi ![]() cùng phương,tức là
cùng phương,tức là ![]() hay
hay
 (IV)
(IV)
với ![]() k > 0 khi
k > 0 khi ![]() cùng hướng, k < 0 khi
cùng hướng, k < 0 khi ![]() cùng phương khác hướng.
cùng phương khác hướng.
Các bất đẳng thức (II’), (III’) gợi ý cho ta có thể chứng minh đẳng thức, bất đẳng thức, giải phương trình, bất phương trình, hệ phương trình hoặc bài toán cực trị.
II. MỘT SỐ VÍ DỤ
1.Ứng dụng trong giải phương trình, bất phương trình và hệ phương trình
a. Giải phương trình
Ví dụ 1: Giải phương trình
![]() (1)
(1)
Lời giải:
ĐK: ![]()
Đặt ![]()
Khi đó ![]()
 .
.
Do đó theo (II1) thì phương trình (1) xảy ra khi ![]() cùng phương
cùng phương
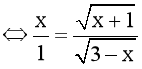 (ĐK: 0< x < 3)
(ĐK: 0< x < 3)

Với nghiệm ![]() < 0 không thỏa mãn đk
< 0 không thỏa mãn đk
Ví dụ 2: Giải phương trình
![]() (2)
(2)
Lời giải:
Đặt ![]()
Ta có: ![]()
Phương trình (2) xảy ra khi ![]() = 3 theo (III’) và từ (IV) ta có hệ phương trình
= 3 theo (III’) và từ (IV) ta có hệ phương trình

b. Giải bất phương trình
Ví dụ 3: Giải bất phương trình
![]() (3)
(3)
Lời giải
ĐK: ![]()
Đặt ![]()
Ta có: 
Theo (II’) ta được: ![]() ,
,
Suy ra bất phương trình (3) chỉ có thể lấy dấu đẳng thức và nhờ (IV) ta được ![]()
Ví dụ 4: Giải bất phương trình
![]() (4)
(4)
Lời giải
ĐK: 
Đặt ![]()
Ta có: ![]()
Theo (II’), ta có bất phương trình (2) luôn được thỏa mãn.
Vậy nghiệm của (2) là 
c. Giải hệ phương trình
Ví dụ 5: Giải hệ phương trình
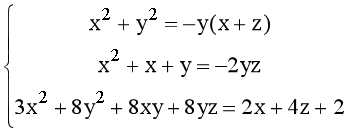 (5)
(5)
Lời giải
Hê đã cho tương đương với

Đặt ![]()
![]()
- Nếu

- Nếu
 cùng phương
cùng phương  . Xét hai trường hợp
. Xét hai trường hợp  ta có nghiệm của hệ
ta có nghiệm của hệ 
Vậy hệ có hai nghiệm là 
Ví dụ 6: Chứng minh rằng hệ sau đây vô nghiệm

Lời giải
Đặt ![]()
Ta có: ![]()
Theo hệ trên, ta có ![]() và
và ![]() .
.
Do đó ![]() điều này mâu thuẫn với (II).
điều này mâu thuẫn với (II).
Vậy hệ trên vô nghiệm.
2. Ứng dụng trong chứng minh đẳng thức và bất đẳng thức
a. Chứng minh bất đẳng thức
Ví dụ 1: Chứng minh rằng với mọi a, b, c ta có
![]() (*)
(*)
Lời giải
Khai triển vế trái: VT = a2bc + ab2c + abc2
Đặt ![]()
Ta có: 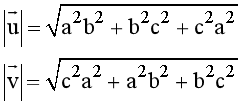
Áp dụng (II) ta được: ![]() (*)
(*)
Lại đặt ![]()
Áp dụng (II) một lần nữa ta được ![]() (**)
(**)
Từ (*) và (**) suy ra (1)
Theo (IV), dễ thấy bất đẳng thức trở thành đẳng thức khi a = b = c.