VÉCTƠ TRONG KHÔNG GIAN
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
1. Định nghĩa và các phép toán
· Định nghĩa, tính chất, các phép toán về vectơ trong không gian được xây dựng hoàn toàn tương tự như trong mặt phẳng.
· Lưu ý:
+ Qui tắc ba điểm: Cho ba điểm A, B, C bất kỳ, ta có: ![]()
+ Qui tắc hình bình hành: Cho hình bình hành ABCD, ta có: ![]()
+ Qui tắc hình hộp: Cho hình hộp ABCD. A¢B¢C¢D¢, ta có: ![]()
+ Hê thức trung điểm đoạn thẳng: Cho I là trung điểm của đoạn thẳng AB, O tuỳ ý.
Ta có: ![]() ;
; ![]()
+ Hệ thức trọng tâm tam giác: Cho G là trọng tâm của tam giác ABC, O tuỳ ý. Ta có:
![]()
+ Hệ thức trọng tâm tứ diện: Cho G là trọng tâm của tứ diện ABCD, O tuỳ ý. Ta có:
![]()
+ Điều kiện hai vectơ cùng phương: ![]()
+ Điểm M chia đoạn thẳng AB theo tỉ số k (k ¹ 1), O tuỳ ý. Ta có:
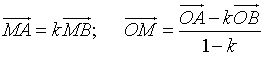
2. Sự đồng phẳng của ba vectơ
· Ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
· Điều kiện để ba vectơ đồng phẳng: Cho ba vectơ ![]() , trong đó
, trong đó ![]() không cùng phương. Khi đó:
không cùng phương. Khi đó: ![]() đồng phẳng Û $! m, n Î R:
đồng phẳng Û $! m, n Î R: ![]()
· Cho ba vectơ ![]() không đồng phẳng,
không đồng phẳng, ![]() tuỳ ý.
tuỳ ý.
Khi đó: $! m, n, p Î R: ![]()
3. Tích vô hướng của hai vectơ
· Góc giữa hai vectơ trong không gian:
![]()
· Tích vô hướng của hai vectơ trong không gian:
+ Cho ![]() . Khi đó:
. Khi đó: ![]()
+ Với ![]() . Qui ước:
. Qui ước: ![]()
+ ![]()
4. Các dạng toán thường gặp:
a) Chứng minh đẳng thức vec tơ.
b) Chứng minh ba vec tơ đồng phẳng và bốn điểm đồng phẳng, phân tích một vectơ theo ba vectơ không đồng phẳng.
+ Để chứng minh ba vectơ đồng phẳng, ta có thể chứng minh bằng một trong các cách:
– Chứng minh các giá của ba vectơ cùng song song với một mặt phẳng.
– Dựa vào điều kiện để ba vectơ đồng phẳng: Nếu có m, n Î R: ![]() thì
thì ![]() đồng phẳng
đồng phẳng
+ Để phân tích một vectơ ![]() theo ba vectơ
theo ba vectơ ![]() không đồng phẳng, ta tìm các số m, n, p sao cho:
không đồng phẳng, ta tìm các số m, n, p sao cho: ![]()
c) Tính tích vô hướng cuả hai véc tơ trong không gian
d) Tính độ dài của đoạn thẳng, véctơ.
+ Để tính độ dài của một đoạn thẳng theo phương pháp vec tơ ta sử dụng cơ sở 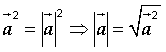 . Vì vậy để tính độ dài của đoạn
. Vì vậy để tính độ dài của đoạn ![]() ta thực hiện theo các bước sau:
ta thực hiện theo các bước sau:
– Chọn ba vec tơ không đồng phẳng ![]() so cho độ dài của chúng có thể tính được và góc giữa chúng có thể tính được.
so cho độ dài của chúng có thể tính được và góc giữa chúng có thể tính được.
– Phân tích ![]()
– Khi đó 

e) Sử dụng điều kiện đồng phẳng của bốn điểm để giải bài toán hình không gian.
Sử dụng các kết quả
· ![]() là bốn điểm đồng phẳng
là bốn điểm đồng phẳng ![]()
· ![]() là bốn điểm đồng phẳng khi và chỉ khi với mọi điểm
là bốn điểm đồng phẳng khi và chỉ khi với mọi điểm ![]() bất kì ta có
bất kì ta có ![]() trong đó
trong đó ![]() .
.
B – BÀI TẬP
Câu 1: Cho hình lăng trụ ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() . Đặt
. Đặt ![]() ,
, ![]() ,
, ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A.  . B.
. B. 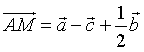 . C.
. C.  . D.
. D.  .
.
 Hướng dẫn giải:
Hướng dẫn giải:
Chọn D.
Ta phân tích như sau:

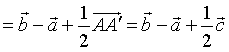 .
.
Câu 2: Trong không gian cho điểm ![]() và bốn điểm
và bốn điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() không thẳng hàng. Điều kiện cần và đủ để
không thẳng hàng. Điều kiện cần và đủ để ![]() ,
, ![]() ,
, ![]() ,
, ![]() tạo thành hình bình hành là
tạo thành hình bình hành là
A. ![]() . B.
. B. ![]() .
.
C.  . D.
. D.  .
.
 Hướng dẫn giải:
Hướng dẫn giải:
Chọn B.
Trước hết, điều kiện cần và đủ để ![]() là hình bình hành là:
là hình bình hành là:
![]() .
.
Với mọi điểm ![]() bất kì khác
bất kì khác ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ta có:
, ta có:
![]()
![]() .
.
Câu 3: Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành. Đặt
là hình bình hành. Đặt ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
 Chọn A.
Chọn A.
Gọi ![]() là tâm của hình bình hành
là tâm của hình bình hành ![]() . Ta phân tích như sau:
. Ta phân tích như sau:
 (do tính chất của đường trung tuyến)
(do tính chất của đường trung tuyến)
![]() .
.
Câu 4: Cho tứ diện ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Đặt
. Đặt ![]() ,
, ![]() ,
, ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A.  . B.
. B.  .
.
C.  . D.
. D.  .
.
Hướng dẫn giải:
 Chọn A.
Chọn A.
Ta phân tích:
 (tính chất đường trung tuyến)
(tính chất đường trung tuyến)
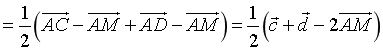
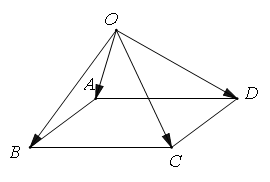
 .
.
Câu 5: Cho hình hộp ![]() có tâm
có tâm ![]() . Gọi
. Gọi ![]() là tâm hình bình hành
là tâm hình bình hành ![]() . Đặt
. Đặt ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. 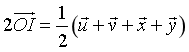 . B.
. B.  .
.
C.  . D.
. D.  .
.
Hướng dẫn giải:
 Chọn D.
Chọn D.
Ta phân tích:
![]() .
.
![]() .
.
![]() .
.
 .
.
Câu 6: Cho hình hộp ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là tâm của hình bình hành
lần lượt là tâm của hình bình hành ![]() và
và ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
A.  .
.
B. Bốn điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() đồng phẳng.
đồng phẳng.
C. ![]() .
.
D. Ba vectơ ![]() ;
; ![]() ;
; ![]() không đồng phẳng.
không đồng phẳng.
 Hướng dẫn giải:
Hướng dẫn giải:
Chọn D.
A đúng do tính chất đường trung bình trong ![]() và tính chất của hình bình hành
và tính chất của hình bình hành ![]() .
.
B đúng do ![]() nên bốn điểm
nên bốn điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() đồng phẳng.
đồng phẳng.
C đúng do việc ta phân tích:
![]()
![]() .
.
D sai do giá của ba vectơ ![]() ;
; ![]() ;
; ![]() đều song song hoặc trùng với mặt phẳng
đều song song hoặc trùng với mặt phẳng ![]() . Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
. Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
Câu 7: Cho tứ diện ![]() . Người ta định nghĩa “
. Người ta định nghĩa “ ![]() là trọng tâm tứ diện
là trọng tâm tứ diện ![]() khi
khi ![]() ”. Khẳng định nào sau đây sai?
”. Khẳng định nào sau đây sai?
A. ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() (
( ![]() ,
, ![]() lần lượt là trung điểm
lần lượt là trung điểm ![]() và
và ![]() ).
).
B. ![]() là trung điểm của đoạn thẳng nối trung điểm của
là trung điểm của đoạn thẳng nối trung điểm của ![]() và
và ![]() .
.
C. ![]() là trung điểm của đoạn thẳng nối trung điểm của
là trung điểm của đoạn thẳng nối trung điểm của ![]() và
và ![]() .
.
D. Chưa thể xác định được.
Hướng dẫn giải:
 Chọn D.
Chọn D.
Ta gọi ![]() và
và ![]() lần lượt là trung điểm
lần lượt là trung điểm ![]() và
và ![]() .
.
Từ giả thiết, ta biến đổi như sau:
![]()
![]() là trung điểm đoạn
là trung điểm đoạn ![]() .
.
Bằng việc chứng minh tương tự, ta có thể chứng minh được phương án B và C đều là các phương án đúng, do đó phương án D sai.
Câu 8: Cho tứ diện ![]() có
có ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Đặt
. Đặt ![]() ;
; ![]() ;
; ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A.  . B.
. B.  .
.
C.  . D.
. D. 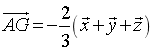 .
.
Hướng dẫn giải:
Chọn A.
 Gọi
Gọi ![]() là trung điểm
là trung điểm ![]() .
.
Ta phân tích:
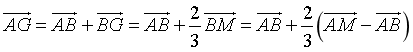
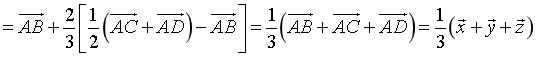 .
.